|
НАУЧНЫЕ РЕЗУЛЬТАТЫ 2012 ГОДА
[Публикации 2012 года]
1. АЛГОРИТМ ОПРЕДЕЛЕНИЯ СОСТАВА СМЕСИ ВЕЩЕСТВ ПРИ НАЛИЧИИ ПРИМЕСЕЙ [наверх]
Ранее описанный алгоритм определения состава смеси веществ на основе однократно зарегистрированного спектра смеси и нечетко заданных спектров компонентов распространен на случай наличия неооднозначно охарактеризованных примесей.
На основании таблицы 1 и анализа особенностей действия алгоритма можно сделать вывод, что определение концентраций выделяемых компонентов смеси вполне возможно даже в случае очень большого фона примесей. Важно, что фон может образоваться молекулами, которые сильно поглощают излучение в тех же областях, что и определяемые соединения (интервал валентных CH-колебаний). Решающую роль в этом случае играет область “отпечатков пальцев”.
Результаты определения концентраций двух выделенных компонентов смеси
из 10 соединений, восемь из которых образуют спектр примеси | Номер
смеси | Метилаллен | Изобутан | транс-Бутен | Бутан | Бутадиен | Бензол | Циклогексан | Δ | | Заданная концентрация | | 3.5 | 4.0 | 0.75 | 2.5 | 1.5 | 3.0 | 0.5 | | 1 | | | | 2.44
2.38
2.27 | 1.52
1.34
1.45 | | | 0.11
0.08
0.10 | | 2 | | | | 2.72
2.63
2.29 | | 2.85
2.83
2.79 | | 0.20
0.18
0.25 | | 3 | | | | | 1.48
1.52
1.73 | 3.11
3.13
3.35 | | 0.19
0.16
0.14 | | 4 | | | | 2.51
2.45
2.01 | | | 0.43
0.45
0.72 | 0.05
0.05
0.09 | | 5 | | | | | 1.45
1.42
1.39 | | 0.503
0.49
0.48 | 0.06
0.05
0.04 | | 6 | | | | | | 3.03
3.12
3.11 | 0.48
0.53
0.55 | 0.2
0.13
0.16 | | 7 | 3.44
3.42
3.45 | 3.98
3.89
3.76 | | | | | | 0.16
0.15
0.18 | | 8 | 3.39
3.37
3.33 | | 0.79
0.75
0.91 | | | | | 0.10
0.09
0.10 | | 9 | | 3.88
3.83
3.89 | 0.95
0.91
0.88 | | | | | 0.09
0.08
0.07 | | 10 | 3.48
3.36
3.38 | | | 2.48
2.39
2.24 | | | | 0.21
0.17
0.17 |
Примечание. Заданная концентрация входящих в состав смеси
толуола, дифенила и этилена 1.8, 0.6 и 1.5 соответственно.
Автоматически решается и задача о границах интервала возможных значений концентраций определяемых соединений. Например, для пары бутан-бутадиен получаем границы доверительного интервала для бутана 2.31—2.46, для бутадиена 1.39—1.46 (малый фон). В случае сильного фона для той же пары имеем 2.23—2.61 и 1.40—1.61. Для пары бутадиен-циклогексан интервалы для малого фона получаются в пределах 1.41—1.45 и 0.49—0.52, а для большого фона 1.36—1.63 и 0.43—0.57. В остальных случаях результаты аналогичные. Границы интервалов оценивались на основании полученных с помощью процедуры бутстрепа гистограмм распределения значений искомых концентраций. Очень важно, что описываемый подход может быть использован для планирования экспериментов, если сформулирована соответствующая аналитическая проблема, а также в условиях, когда состав примеси не известен.
2. ОБЩИЕ ПРИНЦИПЫ ПОСТАНОВКИ И РЕШЕНИЯ ЗАДАЧИ ПРОГНОЗА ХОДА
ФОТОХИМИЧЕСКИХ РЕАКЦИЙ. ФОТОХИМИЯ И ФОТОАНАЛИТИКА [наверх]
Сформулированы базовые принципы прогноза и анализа фотохимических превращений сложных молекул. Эти принципы отражают физическую природу, физико-химические свойства и закономерности наблюдаемого явления, а также учитывают общие особенности постановки и решения квантово-химических задач для сложных молекул (выбор оптимальных моделей, использование эффективных приемов прогностического уровня и пр.). Полученные результаты базируются на количественной теории фотохимических процессов и моделировании кинетики конкретных фотохимических реакций и расчете их квантовых выходов.
Процесс фотохимического исследования неизбежно носит характер последовательных шагов от формирования гипотез о вероятных путях фотопревращения, их конкретизации (сокращение числа возможных вариантов) за счет учета информации о механизме реакции (близкодействие, локальность структурного преобразования, характеристичность колебаний) и оценки на полуколичественном уровне вероятности процессов (да/нет) с учетом «пространственных» запретов и, на конечном этапе, проведения для отобранных гипотез расчета кинетики и квантовых выходов фотохимических реакций.
Разработан и оформлен математически общий алгоритм цепочки. Цель: создание экспертной системы для прогноза вероятности фотохимических реакций и решения аналитических задач
Развиваемые теория и методы расчета дают основания считать, что можно реализовать путь исследования для конкретных практических задач и получать количественные предсказания квантовых выходов на удовлетворительном уровне согласия с экспериментом. Подчеркнем, что для многих фотохимических задач уже достаточно и крайне важно получение оценок по порядку величин: планирование постановки эксперимента, поиск наиболее оптимального пути фотопревращения исходной молекулы в требуемый продукт из большой иерархии возможных и др.
Экспериментальные и вычисленные значения квантовых выходов реакций
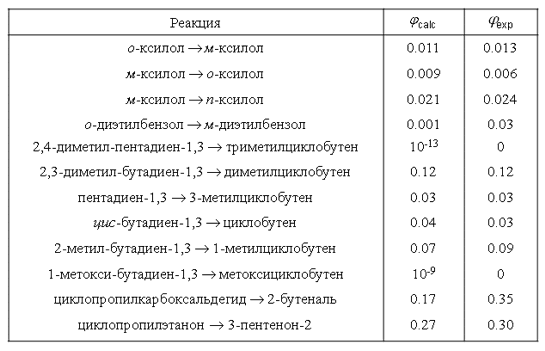
Важным фактором является влияние ангармонизма колебаний комбинирующих в фотопроцессе молекул, который приводит к существенному (на порядок и более) повышению вероятности безызлучательного перехода за счет «примешивания» в волновую функцию реакционного состояния функций обертонных и составных колебаний. Следствием является то, что фотохимические превращения молекул осуществляются преимущественно через низколежащие колебательные уровни возбужденных электронных состояний и, поэтому, для инициации фотохимической реакции нет необходимости использовать оптическую «накачку» в состояния с большими колебательными квантовыми числами. Это следует учитывать при постановке экспериментов, как и возможность (высокую вероятность) реализации многоканальных процессов вследствие многоуровневого резонанса – широкополосное возбуждение может быть эффективнее резонансного. Для сложных многоатомных молекул такая ситуация типична из-за большой плотности состояний. Весь подход распространяется и на термические реакции, если учесть больцмановское заполнение уровней.
3. О ЧИСЛЕННОМ РЕШЕНИИ ЭЛЕКТРОННО-ЯДЕРНОЙ ЗАДАЧИ ДЛЯ МОЛЕКУЛ ПРИ
ИСПОЛЬЗОВАНИИ ИНТЕГРАЛЬНОГО ОПЕРАТОРА ЭЛЕКТРОННО-ЯДЕРНОГО ВЗАИМОДЕЙСТВИЯ [наверх]
Описан алгоритм численного решения ранее предложенного в интегро-дифференциального уравнения Шредингера, в котором оператор электронно-ядерного взаимодействия имеет интегральную форму по ядерному распределению, а само уравнение записывается в разделяющихся переменных электронов и ядер. Выводы сводятся к следующему.
1. Квантование электронно-ядерных движений в молекулярных системах содержательно описывается уравнением Шрёдингера с интегральным потенциалом взаимодействий электронов и ядер, учитывающим реальную химическую структуру молекул, а не физически бесструктурную плазму из точечных электронных и ядерных зарядов, движущихся согласно уравнению Шрёдингера с кулоновскими взаимодействиями частиц.
2. Численное решение уравнения Шрёдингера с интегральным оператором электронно-ядерного взаимодействия выполняется в традиционной схеме метода МО ЛКАО с вычислением дополнительных матричных элементов по колебательным координатам ядер, что связано с расчётом производных второго порядка от функций регулярного поведения в области определения переменных и параметров как в вычислительной схеме «ГАУССИАН», так и в схеме «БЕССЕЛИАН».
3. Предложенный алгоритм решения уравнения Шрёдингера позволяет сформулировать также полуэмпирический вариант теории для крупных молекулярных систем в силу практической возможности задания интерполяционных формул для матричных элементов в значимых для химических процессов интервалах параметров АО и коэффициентов вычислительного алгоритма. Это создает возможности теоретических физико-химических исследований природы химических связей и энергетики сложных молекулярных систем и новых химических соединений.
4. ОБЩАЯ ТЕОРИЯ СТРОЕНИЯ И СВОЙСТВ АТОМОВ И МОЛЕКУЛ [наверх]
1. С помощью многоэлектронного релятивистского уравнения для атома выяснена физическая природа слоистого строения электронных оболочек химических элементов и феноменологического принципа Паули заселения электронных уровней в молекулах. Показано, что решающая роль в распределении электронов по группам принадлежит отталкиванию электронов.
2. Впервые в теории многих частиц получена строгая зависимость кинетической энергии от квадрата углового момента системы частиц, что позволяет в квантовой теории атомов и молекул исследовать спектральные серии уровней энергии по величине сохранившегося углового момента.
3. Рассмотрен вопрос о том, как должна быть поставлена и решена задача об уровнях энергии и волновых функциях молекулы в том случае, когда существенно заполненными являются колебательно-возбужденные состояния (“нагретые” молекулы) и когда нельзя пренебрегать “размазанностью” ядер из-за возрастания амплитуды их колебаний. Показано, что вся проблема учета “размазанности” ядер становится сходной с традиционной, но оказывается ближе к физической природе объекта. Все рассуждения позволяют обосновать ряд важных особенностей традиционного подхода. В частности, получается объяснение известного результата о том, что параметры экспонент Слэтера существенно меньше значений электронных экспонент реальных зарядов ядер. Обычно это связывают лишь с влиянием экранирования поля действием внутренних не валентных электронов. Видно, однако, что это в значительной степени может быть следствием также того, что поле создается не одним сосредоточенным в одной точке зарядом, а несколькими разнесенными в пространстве меньшими по величине. Выясняется, что сглаживание особенностей атомных орбиталей в области близкой к нулю путем замены экспоненциальных функций гауссовыми является вполне рациональной не только с вычислительной, но и с физической точки зрения.
5. ОБ ОПРЕДЕЛЕНИИ СИСТЕМЫ ПАРАМЕТРОВ В ВАЛЕНТНООПТИЧЕСКОЙ СХЕМЕ [наверх]
На примере 36-ти органических соединений, для которых известны абсолютные интенсивности полос в ИК спектрах поглощения, рассмотрен комбинированный метод решения обратной электрооптической задачи. Использовались данные квантово-химических вычислений для нахождения начальных значений электрооптических параметров (ЭОП) и экспериментальные данные об абсолютных интенсивностях полос для определения окончательных величин.
Показано, что наложенные дополнительные условия должны отвечать требованию "близкодействия", т.е. слабой зависимости распределения электронной плотности в замкнутой группировке от движения атомов в прилегающих структурных элементах всей молекулы. В этом случае возможно получение локальных ЭОП µij, быстро уменьшающихся по величине при увеличении расстояния между атомами для координат, отвечающих движениям групп атомов, в которых нет общих.
При использовании комбинированного метода решения обратных электрооптических задач могут получаться хорошо переносимые в ряду соединений ЭОП для замкнутых группировок. Для групп атомов, находящихся в схожих условиях, получаются достаточно близкие значения параметров.
6. МЕТОДИКА ПОСТРОЕНИЯ БАНКОВ ЭЛЕКТРООПТИЧЕСКИХ ПАРАМЕТРОВ
ПРИ РАСЧЕТЕ СПЕКТРАЛЬНЫХ СВОЙСТВ НАНООБЪЕКТОВ [наверх]
Обсуждаются теоретические основания проблемы определения оптимального числа и значений электрооптических параметров для создания банков данных с целью расчета спектральных свойств нанообъектов заданной микроструктуры и решения аналитических задач.
Показано, как может быть поставлена и решена задача определения электрооптических параметров для ряда соединений с учетом переносимости параметров моделей и результатов квантовых расчетов производных от дипольных моментов молекул по нормальным координатам. При решении такой задачи, во-первых, обеспечивается возможность сжатия информации о спектрах в банках данных, так как вместо оцифрованных спектральных кривых надо хранить гораздо меньше параметров (силовых постоянных и электрооптических параметров) для представителей гомологических рядов. Во-вторых, создается база для проведения массовых и быстрых расчетов (компьютерное экспериментирование) ИК спектров без ограничений на размеры молекулярных структур. В-третьих, что практически очень важно, появляются условия решения аналитических задач и создания соответствующих методик в целом ряде областей науки.
7. ПРОГРАММА РАН "ПРОБЛЕМА ПРОИСХОЖДЕНИЯ ЖИЗНИ И СТАНОВЛЕНИЯ БИОСФЕРЫ" [наверх]
Рассмотрен вопрос о некоторых базовых закономерностях образования молекулярного мира на ранних стадиях возникновения Вселенной. Сделан вывод о том, что важнейшим фактором при возникновении сложных молекул в результате флуктуационного образования сгустков атомов или простейших соединений является способность одной и той же совокупности атомов переходить в состояние молекулы в форме громадного числа разнообразных структурных изомеров.
Некоторые из 914 возможных структурных изомеров, имеющих химический состав C7H4.
Линейные участки изображены как изогнутые для наглядности.
Сделан вывод о том, что эволюционное усложнение объектов Вселенной возможно лишь при взаимодополнении случайности и детерминизма. Последний может быть логически последовательно описан средствами общей теории спектров и химических превращений.
| 
