|
НАУЧНЫЕ РЕЗУЛЬТАТЫ 2016 ГОДА
[Публикации 2016 года]
1. КВАНТОВАЯ ТЕОРИЯ МОЛЕКУЛ [наверх]
1.1. Методы моделирования оптических свойств соединений с тяжелыми элементами [наверх]
Рассмотрен вопрос о спиновых мультиплетах в соединениях тяжелых элементов. Построена многоэлектронная релятивистская теория спиновых мультиплетов электронных состояний соединений тяжелых элементов на основе анализа многочастичного релятивистского интегрального уравнения. Определены мультиспинорные базисные функции, необходимые при решении прикладных задач фотохимии и спиновой химии, включая спектральные свойства молекул, на основе многоэлектронного релятивистского волнового уравнения для молекулярных систем.
1.2. Развивающиеся во времени процессы в молекулярном мире [наверх]
Исследование направлено на решение важнейшей задачи современной науки – создание теоретических основ методов описания и прогнозирования молекулярных процессов.
Для описания всех развивающихся процессов в молекулярном мире (внутримолекулярные переходы, химические превращения) разработан общий подход с использованием многомерного пространства с координатами – заселённостями уровней. Пространственные формы молекул и ван-дер-ваальсовых комплексов характеризуются естественными координатами. Построена энергетическая матрица с учётом резонансных состояний и квантовых биений. Предложена единая система дифференциальных уравнений для одновременного описания изменений внутримолекулярных состояний и химических превращений, что позволяет моделировать процессы и изучать их особенности.
Схема сложного многоступенчатого процесса, кинетика которого описывается следующей системой уравнений:
Результат решения системы уравнений с начальными условиями n1(0) = 1, n2(0) = ... = n10 = 0.
1.3. Анализ свойств электронных оболочек больших молекул [наверх]
Рассмотрено решение актуальной задачи об анализе свойств электронных оболочек очень больших молекул. Учитывается принцип близкодействия и существование сравнительно небольших структурных группировок, достаточно мало зависящих от окружения. Предложен метод расчёта состояний электронов в больших молекулах на основе линейных комбинаций одноцентровых функций фрагментов с последующим учётом их взаимодействий. Показано, что вычислительная процедура может быть построена аналогично обычной с использованием ЛКАО.
1.4. Общий подход для решения задачи о ядерных движениях в молекулах [наверх]
Предложен общий подход для решения задачи о ядерных (колебательно-вращательных) движениях в молекулах. Разработан вариационный метод вычисления колебательно-вращательных уровней энергии многоатомной молекулы, базирующийся на определении вращения как состояния с постоянным моментом импульса. Получен очень важный вывод: для колеблющейся молекулы в принципе нельзя точно найти значения уровней энергии на основе одного гамильтониана для вращений. Однако, можно сразу найти значения колебательно-вращательных уровней энергии, воспользовавшись энергетической матрицей, объединяющей колебания и вращения. Принципиально, что подход легко распространяется на случай ангармонических колебаний и колебаний большой амплитуды. Метод позволяет получать значения уровней энергии для любого колебательного состояния с произвольными значениями колебательных квантовых чисел. Это даёт возможность рассчитывать колебательно-вращательные уровни энергии "нагретых" молекул. Тем самым задача решается полностью и с хорошей степенью точности.
1.5. Гамильтониан для электронно-колебательно-вращательной задачи в теории молекул [наверх]
Предложен гамильтониан, описывающий одновременно электронные и колебательные состояния и вращения молекулы как целого. В основе развитого подхода лежит использование обобщённых (естественных) координат для описания электронов и ядер и представления о молекуле как устойчивой геометрической фигуре, где электроны и ядра взаимодействуют по Кулону, а ядра с ядрами – упруго. Показано, что задача об электронно-колебательно-вращательных уровнях энергии формализуется полностью. Всё решение целиком определяется заданием потенциала для колебаний ядер, что соответствует физически корректному образу молекулы как упругой геометрической фигуры. В отличие от обычного подхода (аддитивные слагаемые в гамильтониане для электронных и ядерных состояний) проявляется влияние колебаний ядер на электронные состояния, что отвечает наблюдаемому изотопическому эффекту в электронных спектрах. Вся вычислительная процедура оказывается более простой, чем при традиционном алгоритме. Сохраняется принцип ab initio, только он связан не с выбором базиса, а с формой потенциала для колебаний. Легко совершается переход в расчёте от основных к ридберговским состояниям.
1.6. Гамильтониан для задачи об электронно-ядерных состояниях
нанообъектов конечных размеров с периодической структурой [наверх]
Нанообъекты занимают промежуточное положение между одиночными объектами (молекулы) и бесконечно протяжёнными (полимеры и кристаллы), поэтому требуют создания адекватных методов. Для исследования как основных, так и возбуждённых состояний нанообъектов с периодической структурой предложен гамильтониан, позволяющий находить общее решение в виде линейной комбинации базисных функций в форме нормальных волн. Явно выделяются составляющие, позволяющие легко получать решение с разной степенью точности. Метод пригоден как для анализа конечных, так и бесконечно протяжённых объектов, включающих участки периодической структуры.
2. АНАЛИТИЧЕСКАЯ ХИМИЯ [наверх]
Сформулирована общая постановка задачи количественного спектрального анализа сложных смесей веществ с учетом процессов молекулярного разложения и многомерности спектральных данных; развит математически и физически обоснованный метод решения таких задачи.
2.1. Определение концентрационного состава смесей веществ
и продуктов химических превращений методами многомерной спектроскопии.
Алгоритм обработки экспериментальных данных [наверх]
Проанализированы практически важные варианты задачи количественного безэталонного спектрального анализа в ее наиболее общей постановке, включая многомерные и зависящие от времени спектральные данные. Предложены и развиты альтернативные подходы, позволяющие решать задачу в самом общем случае изменяющихся во времени спектров индивидуальных компонентов и их смеси, а также концентраций. Это позволяет получить как искомый аналитический ответ о временных зависимостях концентраций (в форме гистограмм распределения их значений) и полное представление о ходе химической реакции, так и определить вероятности химических взаимопревращений.
При выполнении количественного анализа необходимо определять не только наиболее вероятные значения концентраций компонентов смеси, но и погрешности полученного решения. Это требование обусловлено всегда присутствующими экспериментальными и теоретическими "погрешностями", связанными с особенностями проведения эксперимента, выбором теоретических моделей молекул, сформулированной исходной гипотезы о предполагаемом составе смеси и другими факторами. Показано, что варьирование спектральных данных может осуществляться, в частности, с помощью "шумовой" добавки, моделирующей возможные (всегда присутствующие) погрешности не только спектральной теории и эксперимента, но и выдвинутой исходной гипотезы о предполагаемом составе анализируемой смеси.
Получаемые значения концентраций устойчивы к возможным погрешностям задания исходных спектральных данных. Увеличение числа компонентов в смеси не меняет полученных выводов о сходимости решения аналитической задачи и его устойчивости.
| Пример результатов модельных расчетов | 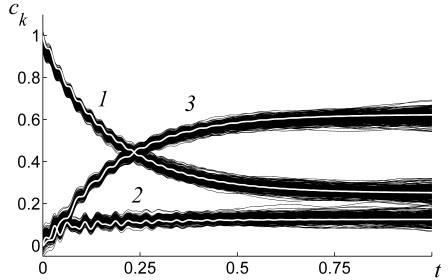 | 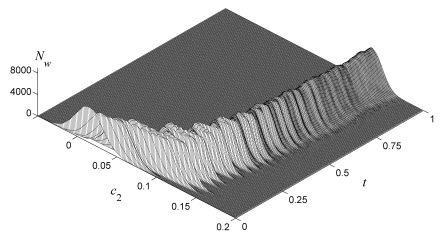 | Временные зависимости найденных
концентраций компонентов 1, 2 и 3 смеси | Гистограмма распределения значений
концентраций компонента 2 |
2.2. Фотохимические превращения при длительных оптических воздействиях [наверх]
Фотохимические процессы широко распространены в природе и имеют широкий диапазон применения. Спектральные проявления таких процессов, как и сам ход превращений, чрезвычайно разнообразны, и существенно зависят, в частности, от изменения условий возбуждения (импульсное, длительное и т.д.), которые очень сильно влияют на квантовый выход реакции и ее спектральные проявления.
Рассмотрены особенности формирования системы кинетических уравнений при моделировании таких процессов. Показано, что при моделировании ситуации непрерывного облучения светом необходимо в системе уравнений вводить два канала перекачки населённости через резонансный уровень. Эти каналы, конечно, не являются независимыми, так как они связаны через основные уровни.
Исследованы особенности фотохимических превращений и их моделирования при длительных непрерывных световых воздействиях.
При импульсном возбуждении стационарные значения концентраций при слабом взаимодействии комбинирующих структур малы из-за быстрой по сравнению со структурными превращениями релаксацией возбужденных состояний. Постоянное оптическое возбуждение качественно меняет ситуацию. Длительная "накачка" приводит к постоянному заселению резонирующих состояний комбинирующих молекулярных структур и квантовый выход не равен нулю даже при очень малых частот квантовых биений. Так, например, для реакций 2,4-диметил-пентадиен-1,3 → триметилциклобутен и 2,4-диметил-пентадиен-1,3 → триметилциклобутен при импульсном возбуждении квантовый выход равен нулю, а при постоянном возбуждении количество продукта оказывается большим и составляет величину порядка 0.65.
Для быстрых реакций кинетика процесса носит с высокой степенью точности экспоненциальный характер. В случае медленных реакций изменение во времени качественно меняется, возникают осцилляции концентраций, ярко проявляющиеся в стационарном состоянии молекулярной системы. Величины осцилляций могут быть весьма значительными (порядка 25% и более). Продолжительное оптическое воздействие в случае медленных реакций может привести не только к значительному по величине выходу продукта, но и к появлению хорошо известного эффекта колебательных реакций.
В случае медленных реакций выход продукта существенно зависит от момента времени прекращения фотовозбуждения. Выбор оптимального времени светового воздействия является существенным фактором при планировании эксперимента с целью получения требуемого количества продукта. Молекулярное моделирование позволяет оценить эту величину априори.
2.3. Постановка задачи количественного анализа смесей для двухмодальных спектральных данных в случае однократных измерений [наверх]
Дана математическая формулировка задачи о концентрационном составе смеси по данным многомерной спектроскопии при наличии единственного эксперимента – задачи о смеси неизвестного числа неизвестных компонентов с неизвестными концентрациями.
Показано, что в качестве критерия корректности исходной гипотезы и результата анализа можно использовать как величину разброса получаемых концентраций, определяемую по соответствующим гистограммам распределений, так и дисперсию метода наименьших квадратов (МНК).
Результаты модельных расчетов показали, что характер зависимости дисперсии МНК от уровня шума в спектральных данных близок к линейному в достаточно большом интервале значений величины шума. В совокупности с заданным при постановке задачи уровнем требуемой точности получаемого решения это позволяет характеризовать корректность как сформулированной гипотезы, так и конечного результата анализа.
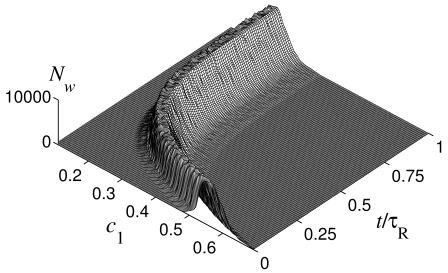 | 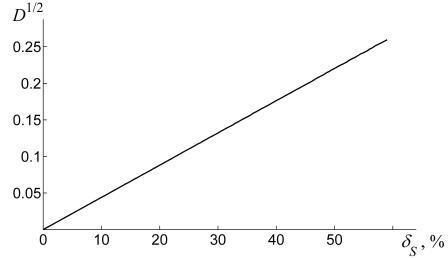 | Гистограмма распределения значений
концентраций | Взаимосвязь дисперсии МНК D
и погрешности исходных спектральных
данных δS |
3. ПРОЦЕССЫ В СЛОЖНЫХ БИОХИМИЧЕСКИХ СИСТЕМАХ
(ГЕОХИМИЯ, ЭКОЛОГИЯ, ЭВОЛЮЦИЯ БИОСФЕРЫ И ДР.) [наверх]
3.1. Разработка способов количественного оценивания хода эволюции
в мире органических молекул [наверх]
Исследование направлено на решение важнейшей задачи современной науки – объяснение эмпирически наблюдаемых закономерностей эволюции молекулярного мира на основе базовых физических законов и теорий.
Изучены закономерности молекулярных превращений в условиях конденсированной среды, в которой всегда присутствуют и играют принципиальную роль межмолекулярные взаимодействия. Рассмотренные примеры продемонстрировали физику появления энергетических зон.
Показано, что энергетические особенности конденсированной среды (появление зон) могут привести к инициирующему химическую реакцию постепенному накоплению внутренней энергии в реакционных центрах за счёт последовательных тепловых столкновений с частицами среды. Для этого не требуются высокие температуры.
Накопление энергии в реакционных центрах молекул 1-гексена (1) и 1-додекена (2)
при последовательных столкновениях с частицами среды в зависимости от номера удара
4. ТАУТОМЕРИЯ ОСНОВАНИЙ НУКЛЕИНОВЫХ КИСЛОТ [наверх]
Продолжено изучение таутомерии оснований нуклеиновых кислот (ОНК). Рассмотрена возможность определения таутомерного состава ОНК в разных фазовых состояниях методами оптической спектроскопии. С целью определения возможности образования таутомера 7-азаиндола выполнен расчет электронных спектров димера 7-азаиндола и димера таутомера для двух моделей, отличающихся симметрией. Вычисленные спектры флуоресценции хорошо согласуются с экспериментом. Показана возможность неоптических переходов между уровнями и таутомерного превращения.
Вычислены спектры флуоресценции двух длинноволновых электронных переходов S0 ← 1Lb и S0 ← 1La незаряженной и цвиттер-ионной формы L-триптофана (Trp) в водном растворе и комплексе Trp с молекулой воды методом DFT в приближении Франка-Кондона. Определены геометрические параметры Trp в электронно-возбужденных состояниях и выполнена интерпретация колебательной структуры вибронных спектров. Показано, что определяющее влияние на флуоресценцию и формирование колебательной структуры электронных спектров оказывает взаимное расположение структурных фрагментов аланина (R-Ala) и индола (R-In).
5. СПЕКТРЫ КОМБИНАЦИОННОГО РАССЕЯНИЯ УГЛЕРОДНОЙ НАНОТРУБКИ [наверх]
Исследованы спектры комбинационного рассеяния углеродной нанотрубки. Методом конфокальной спектроскопии КР локализован гетеропереход в дефектной углеродной нанотрубке, наличие которого свидетельствует об изменении хиральности нанотрубки и типа ее проводимости. Проведен расчет и выполнена интерпретация колебательных КР спектров изолированного молекулярного фрагмента одностенной углеродной нанотрубки без дефекта и включающего дефекты Стоуна–Уэйлса, двух пентагональных и двух гептагональных ячеек. Рассмотрено влияние дефектов на форму полос компонент G+ и G–, вид которых позволяет определить тип проводимости нанотрубки.
6. ЭКСПЕРИМЕНТАЛЬНОЕ ИЗМЕРЕНИЕ ШТАРКОВСКОГО УШИРЕНИЯ ЛИНИЙ MN I
С ПОМОЩЬЮ «ПРОТЯЖЕННОЙ» ЛАЗЕРНОЙ ИСКРЫ [наверх]
Проведены экспериментальные измерения штарковского уширения спектральных линий Mn I для мультиплетов z6P° → a6S и z6D° → a6D в индуцированной лазером «протяженной» лазерной искре. Измеренное штарковское уширение резонансного мультиплета z6P° → a6S уменьшается от 0.075 Å для его первого компонента до 0.055 Å для последнего, в то время как штарковское уширение компонентов мультиплета z6D° → a6D увеличивается от 0.095 Å до 0.125 Å. Смещение линий мультиплетов не наблюдалось.
| 
