Основные научные результаты

 

Основные научные результаты (pdf)

ОСНОВНЫЕ НАУЧНЫЕ РЕЗУЛЬТАТЫ

В данном разделе дана достаточно подробная сводка основных результатов, полученных сотрудниками лаборатории, аспирантами и представителями других учреждений, участвовавшими в проведении совместных работ за время функционирования исследовательского коллектива.

Все подразделы заканчиваются ссылками на публикации, в которых наиболее полно изложены соответствующие разделы. Как правило, это монографии. Они не содержат обзоров литературы, но целиком написаны на базе оригинальных материалов и подводят итоги крупных этапов развития основных направлений. В ряде случаев указываются отдельные статьи, если их содержание не отражено в монографии или они опубликованы после выхода книг.

A. ФИЗИЧЕСКАЯ ТЕОРИЯ СТРОЕНИЯ МОЛЕКУЛ [наверх]

A1. Базовые положения квантовой теории молекул [наверх]

A1a. Постановка квантовых задач [наверх]

Проведена ревизия базовых положений квантовой теории строения и свойств многоатомных молекул. На основе принципа математического отображения общепринятых моделей многоатомных молекул рассмотрены основные вопросы постановки квантовых задач.

Обращено внимание на то, что, подобно брутто-формуле, адекватное ей уравнение Шредингера, в котором учитываются только атомный состав соединения и кулоновские взаимодействия между электронами и ядрами, не является достаточным для конкретизации проблемы и не позволяет выделить, пользуясь только «первыми принципами» квантовой механики, желаемые структурно-изомерные формы из всего возможного их множества (более 10⁶ для системы из 30 атомов).

Вполне определённая постановка задачи возможна, если, отправляясь от структурной формулы и соответствующей матрицы смежности, сформировать энергетическую (гамильтонову) матрицу и воспользоваться матричной формулировкой квантовой механики. Такой подход не есть результат поиска приближённого решения дифференциального уравнения Шредингера. Это другая самодостаточная формулировка задачи.

Предложено новое уравнение Шредингера, адекватное математическому отображению молекулярной модели в форме пространственной фигуры с определённым расположением ядер и с учётом их квантовой «размазанности». Локализация движения ядер обеспечивается априорным заданием характеристик потенциальной «ямы». Однозначно связанная с ней колебательная волновая функция позволяет записать учитывающие «размазанность» ядер уравнения Шредингера в разделяющихся переменных – координатах электронов и ядер. В волновых функциях и собственных значениях электронных слагаемых в таких гамильтонианах автоматически учитываются квантовые характеристики состояний ядер. Это имеет аналогию с «мягким» неадиабатическим приближением в традиционной теории, но является более общим. Подход позволяет учитывать особенности движений ядер не только внутри одной «ямы», но и в «ямах» с двумя и более минимумами (инверсия, цис-, транс-изомерия, внутреннее вращение и др.)

Показано, что с помощью наборов базисных собственных электронно-колебательных функций при разных совокупностях колебательных квантовых чисел можно построить энергетическую матрицу, охватывающую как все учитываемые при постановке задачи электронно-колебательные состояния одной изомерной формы, так и нескольких изомерных форм.

Это позволяет в дальнейшем использовать такую матрицу не только для анализа вероятностей оптических переходов (спектры), но и безызлучательных (химические превращения). Найдены выражения для всех необходимых матричных элементов и указаны способы их вычисления.

Сделан вывод, что в общей квантовой теории строения молекул и молекулярных процессов основанные на матрицах (Гайзенберг) и дифференциальных операторах (Шредингер) варианты квантовой механики выступают не как эквивалентные, а как взаимодополняющие (по Бору).

Весь новый подход отличается от существующего большей логической строгостью и большей простотой вычислений, которые могут быть произведены почти без изменения развитых математических процедур.

Принципиальным является возможность введения единой системы физически наглядных параметров (характеристики «ямы» основного состояния), позволяющих непрерывно воздействовать на колебательные и вибронные уровни энергии и волновые функции. Это даёт возможность ставить и решать разнообразные (спектральные и др.) обратные задачи и уточнять значения электронно-колебательных уровней энергии и характеристики волновых функций, добиваясь хорошего согласия с экспериментом. В традиционной теории такие возможности отсутствуют. Опора непосредственно на экспериментальные данные об ИК и КР спектрах и геометриях молекул и знание их вариаций создаёт также возможность априорной оценки степени достоверности прогноза различных вычисляемых характеристик молекул и более сложных молекулярных образований.

1. Грибов Л.А., Баранов В.И. Теория и методы расчета молекулярных процессов: спектры, химические превращения и молекулярная логика. М: «КомКнига», 2006, 480 с.
2. Грибов Л.А. Элементы квантовой теории строения и свойств молекул. Долгопрудный: Издательский Дом «Интеллект», 2010, с. 312.
3. Грибов Л.А. О некоторых базовых положениях при постановке квантовых задач в теории строения молекул и молекулярных превращений. Журнал структурной химии, 2010, Т. 51, № 4, С. 631-643.
4. Грибов Л.А. Новая форма электронно-ядерного гамильтониана и энергетической матрицы в теории строения и свойств молекул. Журнал структурной химии, 2010, Т. 51, № 5, С. 841-845.
5. Грибов Л.А., Прокофьева Н.И. Матричные элементы для дипольных переходов при постановке квантовой задачи для молекул с ограничениями на движения ядер. Журнал структурной химии, 2011, Т. 52, № 5, С. 871-878.
6. Грибов Л.А., Прокофьева Н.И. Электронно-колебательная задача для молекул с инверсионными движениями. Журнал структурной химии, 2011, Т. 52, № 5, С. 1019-1021.

A1b. Задача о движении электрона в кулоновском поле многих центров [наверх]

Дано решение задачи о движении электрона в кулоновском поле многих центров притяжения.

Эта задача является фундаментальной модельной задачей квантовой химии, аналогичной задаче об атоме водорода в атомной физике. Решение одноэлектронной задачи для многоцентрового кулоновского поля имеет одинаковый характер как в нерелятивистском приближении, так в релятивистской квантовой модели. Показано, что точное решение уравнения Шрёдингера (уравнения Дирака) всегда можно представить в виде линейной комбинации атомных орбиталей (биспиноров), которые могут быть вычислены в виде сходящихся рядов по водородоподобным функциям атомов.

Данное решение дает обоснование традиционному в квантовой химии эвристическому методу МО ЛКАО, основанному на приближении одноэлектронного решения. Алгоритм вычисления волновых функций электрона приводится к алгебраическому уравнению для коэффициентов ЛКАО, в ходе решения которого определяются параметры экспонент АО (параметры Слэтера). Параметры Слэтера в данном решении вычисляются как функции положений ядер молекулы, обеспечивая тем самым необходимую гибкость волновых функций при изменении ядерной конфигурации молекулы, а также правильное асимптотическое поведение электронной плотности при распаде молекулы на фрагменты.

Так, к примеру, в простейшей молекулярной системе H₂⁺ при слиянии ядер получаем спектр и волновые функции иона гелия с соответствующими параметрами экспоненты, а при бесконечно большом межъядерном расстоянии получается спектр атома водорода.

Анализ одноэлектронного решения для многоатомной молекулы дает возможность простыми вычислительными средствами систематически изучить основные особенности электронного спектра сложной молекулярной системы (его нижнюю числовую границу) в зависимости от геометрии молекулярной системы.

Показано, что спектр многоэлектронной системы состоит из решетчатых зон энергетических уровней со структурой, определяемой обменными интегралами многоконфигурационной задачи. Данный результат справедлив как в нерелятивистской, так и в релятивистской квантовой химии.

Разработан эффективный метод вычисления многоцентровых молекулярных интегралов квантовой химии в базисе атомных орбиталей (АО) экспоненциального вида. Метод основан на свойствах функций Бесселя, их класса, имеющего экспоненциальную асимптотику на бесконечном радиусе, т.е. функциях Макдональда, которые при полуцелом индексе являются элементарными функциями в виде произведения многочлена и экспоненты от радиуса. Этим классом функций можно заменить все АО экспоненциального вида, которые также являются произведениями многочлена и экспоненты от радиуса.

Сферическая приведенная функция Бесселя является произведением функции Макдональда на телесную атомную гармонику. Доказано, что произведение сферических функций Бесселя на разных центрах можно заменить интегральным представлением в виде интеграла по единичному отрезку от сферической функции Бесселя суммарного индекса с аргументом в виде суммы квадратов аргументов функций Бесселя в исходном произведении, что позволило представить двухцентровое распределение через одноцентровое. Тем самым данное представление весьма напоминает теорему о приведении произведения гауссовых орбиталей к одной гауссовой функции от аргумента в виде суммы квадратов аргументов исходных гауссианов. Однако метод «БЕССЕЛИАН» позволяет получить приближенные аналитические формулы многоцентровых интегралов для построения теории межмолекулярных взаимодействий, при которых целесообразно сохранять экспоненциальную асимптотику АО на больших расстояниях от атомов. Кроме этого бесселевский базис позволяет использовать более широкий класс функций с более резким (сингулярным) поведением в начале координат, свойственным s-функциям в релятивистской модели движения электронов вблизи тяжелых ядер.

1. Новосадов Б.К. Методы решения уравнений квантовой химии. Основы теории молекулярных орбиталей. М.: Наука, 1988. 184 с.
2. Novosadov B.K. Besselian: calculation of multicenter matrix elements. Journ. Molec. Struct. (Theochem). 2003. Vol.665. P. 55-81.
3. Новосадов Б.К. Методы математической физики молекулярных систем. М.: Книжный дом «ЛИБРОКОМ», 2010. 384 с.

A1c. Квантовая теория соединений с тяжёлыми элементами [наверх]

Предложена новая постановка задачи и развита теория квантовохимического исследования электронных спектров соединений с тяжелыми элементами. По-новому сформулирована теория спиновой химии, в которой в отличие от прежних одночастичных подходов развит многочастичный метод исследования спиновой плотности. Теория опирается на достижения и понятия релятивистской квантовой механики систем многих частиц. Новые результаты связаны с переформулированием квантовых уравнений для быстрых электронов в тяжелых атомах и развитием новых эффективных численных методов расчета энергетических уровней и электронных плотностей молекул.

Учитывая потребности аналитической химии элементов нижней половины таблицы Менделеева, а именно, предварительный прогноз оптических и химических свойств соединений с тяжелыми элементами с целью спектрального анализа, идентификации коротко живущих изотопов и создания безопасных методик их использования, сформулирована новая постановка задачи и развита теория квантовохимического описания и моделирования этих сложных систем. Пример такого рода соединений приведен на рисунке.

Органотитановое соединение, используемое при разработке пртивоопухолевых лекарств.

A1d. Релятивистская теория многоэлектронных систем [наверх]

Разработана релятивистская теория многоэлектронных систем, позволяющая исследовать стационарные электронные состояния тяжелых и сверхтяжелых элементов и содержащих эти элементы молекул. Теория позволяет проводить моделирование химических свойств тяжелых элементов.

Получено фундаментальное решение уравнения Дирака для электрона во внешнем поле. Решение имеет вид экспоненты от релятивистской классической функции действия. Соответствующая фундаментальная волновая функция может быть представлена в виде суммы по квантовым состояниям электрона (фурье-разложения).

Таким образом, получена аналитическая связь классической и квантовой механик, причем классические объекты наблюдаются в опытах по рассеянию света или частиц, а квантовые состояния обнаруживаются при фурье-анализе объекта, т.е. с помощью спектральных методов или неупругого рассеяния света или частиц, при котором проявляются собственные фурье-составляющие объекта физического наблюдения. Аналогичный результат обобщается на систему многих электронов.

1. Новосадов Б.К. Методы математической физики молекулярных систем. М.: Книжный дом «ЛИБРОКОМ», 2010. 384 с.

A1e. Аналитический метод решения релятивистских уравнений [наверх]

Разработан аналитический метод решения полученных уравнений релятивистской квантовой химии для атомов тяжёлых элементов. Метод использует ряд Фробениуса по гиперрадиусу электронных координат для волнового мультиспинора атома и позволяет последовательно вычислить члены ряда. Найденные релятивистские уравнения квантовой химии исследованы в импульсном пространстве электронов, в котором они представляют собой интегральные уравнения Фредгольма.

Получена приближённая релятивистская модель в виде нового скалярного многоэлектронного уравнения для атомно-молекулярной системы, учитывающая как релятивистскую кинематику движения электронов, так и их спиновые свойства.

Показано, что слоистая структура атома обусловлена в первую очередь отталкиванием электронов. Более детальное строение электронной оболочки атома связано с двумя конкурирующими взаимодействиями релятивистской природы, а именно, притяжением магнитных моментов электронов, приводящим к стягиванию электронной плотности атома к ядру, и отталкиванием указанных моментов электронов при определенной их ориентации относительно друг друга. Это приводит к разрыхлению электронной структуры тяжелого атома и появлению химических свойств многовалентности.

Существенно новым элементом в развитом подходе является многочастичная структура волновой функции, позволяющая избежать артефактов одночастичных моделей электронной оболочки атома, до сих пор применявшихся в теории атома.

Метод имеет перспективу применения в квантово-химических исследованиях электронных структур и спектро-химических свойств молекул любого атомного состава.

1. Новосадов Б.К. Аналитическая механика атома. М.: Нобель Пресс. 2014. 323 с.

A1f. Прочие вопросы квантовой теории строения молекул [наверх]

Для характеристики химических связей для молекул произвольного строения предложено строить карты значений проекций векторов сил, действующих на ядро со стороны различных участков электронной плотности, на вектор силы отталкивания данного ядра от всех остальных. Это позволяет наглядно выделить наиболее значимые для связывания молекулы участки общего электронного облака.

Впервые обращено внимание на то, что устойчивые каркасные молекулы, в которых атомы расположены на некоторых замкнутых поверхностях, ограничивающих объём (например, фуллерены), образуются за счёт различий электронных плотностей вне и внутри этих поверхностей.

Предложен метод расчёта электронных уровней энергии и волновых функций молекулярных объектов любой сложности на основе наложения волновых функций молекул, фрагменты которых входят в общую структуру соединения. Метод позволяет легко формировать полную энергетическую матрицу, которая получается сильно разреженной и содержит легко вычисляемые недиагональные матричные элементы. Проблема имеет важное значение для анализа нанообъектов.

Решена важная проблема об использовании избыточного базиса в задаче об электронных состояниях. Метод базируется на применении прямоугольных матриц при приведении особенной матрицы интегралов перекрывания и энергетической матрицы одновременно к диагональному виду.

1. Gribov L.A., Klimova T.P., Raichstatt M.M. Volume conjugation in electron–deficient polyhedral molecules. Journal of Molecular Structure, 1979, v. 56, p. 125-138.
2. Gribov L.A., Raichstatt M.M. Force density method for chemical bond characterization. Journal of Molecular Structure, 1989, v. 183, p. 121-133.
3. Gribov L.A., Novosadov B.K. Use of overcomplete basis sets in quantum-chemical calculations. Journal of Molecular Structure, 1986, v. 136, p. 387-389.
4. Грибов Л.А., Муштакова С.П. Квантовая химия: Учебник. – М.: Гардарики, 1999, 390 с.
5. Грибов Л.А. Фрагментный метод расчёта характеристик электронных состояний очень сложных молекул. Журнал структурной химии, 2008, т. 49, № 1, с. 7-12.

A2. Теория и методы расчёта ИК и электронно-колебательных спектров
многоатомных молекул, полимеров и кристаллов [наверх]

Теория оптических молекулярных спектров является центральной частью общей теории строения и свойств многоатомных молекул. Она имеет и громадное практическое значение.

В течение более чем 30 лет большая группа исследователей под руководством проф. Л.А. Грибова целенаправленно занималась развитием общей теории и методов расчета оптических спектров сложных молекул и полимеров, созданием удобных с точки зрения использования ЭВМ вычислительных алгоритмов и программ и испытанием их на большом числе конкретных примеров.

Всего в этом направлении было опубликовано более 400 статей как в специальных журналах АН СССР и РАН, так и ведущих зарубежных, 10 сборников с текстами программ для ЭВМ (депонированные издания общим объемом более 100 печатных листов), 18 монографий. Список важнейших монографий и наиболее важных обобщающих статей приводится ниже в конце разделов. Было сделано большое число пленарных и больших секционных докладов на самых престижных международных и отечественных конгрессах и конференциях.

Характерной особенностью этих работ являлось подчинение их одной цели — созданию целостного "здания" теоретической молекулярной спектроскопии, взаимосвязанного в своих отдельных частях и "удобного для проживания" в нем не только теоретиков, но и, главным образом, экспериментаторов, непосредственно заинтересованных в получении конкретных выводов о свойствах изучаемых ими методами молекулярной спектроскопии систем.

Основные полученные в лаборатории результаты по данному направлению сводятся к следующим.

A2a. Общая теория спектров и теория колебаний атомов молекул [наверх]

Сформирован математический аппарат теории, проникнутый единством подхода.

Строго решена задача о построении гамильтониана молекулы в системе точных естественных координат без ограничений на характер внутренних движений атомов.

Предложен простой общий способ вычисления матричных элементов, возникающих при переходе от декартовых координат к специальным криволинейным (естественным). Введены новые типы координат: смещения центров масс выделенных атомных группировок, изменения углов, построенных на центрах атомов и центрах масс, координаты согласованных движений групп атомов при внутренних вращениях и конформационных перестройках и др.

Развита техника автоматического перехода от избыточной системы исходных естественных координат к их независимым линейным комбинациям и далее к нормальным с использованием преобразований координат, описываемых не квадратными, как обычно в теоретической механике, а прямоугольными матрицами. Такой подход оказался очень эффективным не только в теории колебательных, но и электронно-колебательных спектров.

Для введения координат симметрии и молекулярных орбиталей симметрии предложен простой способ перехода к таким координатам и орбиталям на основе использования свойств циркулянтных матриц и прямых (кронекеровских) произведений как исходных, так и преобразующих матриц. Введено важное для понимания физики колебаний понятие направляющих векторов симметрии и выяснен их смысл.

Детально изучена физическая природа характеристических колебаний и сформулированы условия характеристичности не только по положениям (частотам) полос и линий в спектрах, но и по их интенсивностям и поляризациям. Установлена иерархия видов характеристичности.

Создана новая техника решения обратных спектральных задач с подавлением расходимости за счет специальных штрафных функций. Обратные задачи решаются при дискретном сопоставлении экспериментальных и вычисленных полос и линий поглощения с использованием интегральных характеристик, а также методов сравнения теоретических и экспериментальных спектральных кривых.

• Список публикаций смотрите после раздела Ангармоническая задача и внутреннее вращение

A2b. Теория интенсивностей в ИКС и СКР [наверх]

Введён обобщающий оператор взаимодействия электромагнитного поля и молекулы, учитывающий как резонансное поглощение падающей электромагнитной волны, так и одновременное действие волн стоксова и антистоксова рассеяния. Это действие также трактуется как резонансный эффект, связанный с тем, что общее электромагнитное поле имеет характер модуляций (биения). Оператор пригоден для описания как обычного, так и резонансного КР.

В области теории интенсивностей в ИКС получены удобные для практических расчётов и получения общих следствий формулы для первых и вторых производных от дипольного момента молекулы по нормальным координатам.

Выяснен смысл перехода к координатам симметрии и сформулированы наглядные векторные правила отбора активных колебаний по симметрии. Решена задача об использовании зависимых координат. Сформулированы критерии характеристичности для фундаментальных, обертонных и составных полос поглощения. Указаны способы решения соответствующих обратных спектральных задач с учётом априорных ограничений. Найдены общие зависимости интенсивностей основных переходов, обертонов и составных частот от числа одинаковых групп в молекулах (это имеет принципиальное значение для решения важного класса аналитических спектрохимических проблем) и др. Впервые в литературе проведены регулярные расчёты электрооптических параметров и показана переносимость их в ряду молекул, содержащих сходные структурные группировки.

Сформулирована последовательная квантовая теория дипольных моментов связей и производных от них по естественным координатам и проведены прямые квантовые расчёты этих величин. Аналогичная работа проделана в теории спектров комбинационного рассеяния.

Разработана методология и техника расчётов спектральных кривых, которые можно непосредственно сопоставить с экспериментом в условиях многочисленных наложений и частичных перекрытий спектральных полос и линий, и накоплен не имеющий аналога в мире расчетный материал, частично представленный в опубликованных монографиях и содержащийся в базе данных программного комплекса LEV.

Рассчитанные ИК спектры сложных соединений показаны на рисунках.

    

• Список публикаций смотрите после раздела Ангармоническая задача и внутреннее вращение

A2c. Ангармоническая задача и внутреннее вращение [наверх]

Предложен прямой вариационный метод решения ангармонических задач в базисах гармонических, "уширенных" гармонических и смешанных морзевско-гармонических функций. Это привело к созданию эффективного математического оформления всего подхода и универсальных программ для ЭВМ, вполне пригодных для проведения массовых практических расчётов. Пример расчёта спектра молекулы хлорэтана в области обертонов показан на рисунке.

Предложен вариационный метод решения ангармонических задач в теории колебаний молекул в криволинейных координатах (центрально силовые) с точным учётом кинематической ангармоничности. Простота вычислительных процедур позволяет применять подход к анализу состояний крупных молекул. Метод имеет важное значение при постановке и решении задач безэталонного спектрального анализа.

Важным видом внутренних движений в молекулах является внутреннее вращение. Дано полное решение этой проблемы с учётом взаимодействий колебаний и внутренних вращений и вычисления интенсивностей линий, отвечающих соответствующим переходам между уровнями энергии.

1. М.В. Волькенштейн, Л.А. Грибов, М.А. Ельяшевич, Б.И. Степанов. Колебания молекул.Изд. 2, Наука, Главн. ред физ-мат., Москва, 1972, 699 с.
2. Л.А. Грибов. Теория инфракрасных спектров полимеров. Наука, Главная редакция физ.-мат. литературы, Москва, 1977, 240 с.
3. Л.А. Грибов, В.А. Дементьев, А.Т. Тодоровский. Интерпретированные колебательные спектры алканов, алкенов и производных бензола. Наука, Москва, 1986, 495 с.
4. Л.А. Грибов, В.А. Дементьев, О.В. Новоселова. Интерпретированные колебательные спектры углеводородов с изолированными и сопряженными кратными связями. Наука, Москва, 1987, 471 с.
5. М.Э. Эляшберг, Ю.З. Карасев, В.А. Дементьев, Л.А. Грибов. Интерпретированные колебательные спектры углеводородов - производных циклогексана и циклопентана. Наука, Москва, 1988, 375 с.
6. L.A. Gribov, W.J. Orville–Thomas. Theory and methods of calculation of molecular spectra. John Wiley and Sons, Chichester, New York, 1988, 636 p.
7. Л.А. Грибов, А.И. Павлючко. Вариационные методы решения ангармонических задач в теории колебательных спектров молекул. Наука, Москва, 1998, 334 с.
8. Л.А. Грибов. Колебания молекул. М.: Книжный дом «ЛИБРОКОМ», 2009, 544 с.

A2d. Теория ИКС полимеров [наверх]

Полимеры (одномерные цепи), полимерные двумерные плёнки и молекулярные кристаллы (трёхмерные периодические структуры) являются объектами, широко исследуемыми методами ИК спектроскопии.

Развит новый метод расчета спектров, пригодный как для работы с регулярными полимерными объектами большой протяженности, так и с олигомерами малой длины. Задачу удалось решить за счёт перехода на первом этапе (нулевое приближение) к нормальным стоячим волнам, что можно сделать одинаковым способом для цепей любой длины, и путём учёта взаимодействий между этими волнами на втором этапе (переход к первому приближению).

Предложенный подход распространен на сополимеры, двумерные и трёхмерные (молекулярные кристаллы) полимерные структуры, а также на важный случай исследования поведения молекул или плёнок на поверхности кристалла.

Созданная теория практически без изменений может быть перенесена на электронные состояния и использована для расчётов зонной структуры твёрдых тел с учётом плотности заполненных и незаполненных состояний. Для этих целей предложен вариант, обеспечивающий решение электронной задачи в приближении Хартри-Фока.

1. Л.А. Грибов. Теория инфракрасных спектров полимеров. Наука, Главная редакция физ.-мат. литературы, Москва, 1977, 240 с.
2. Л.А. Грибов, С.Д. Демухамедова. Метод расчета колебательных спектров привитых и блоксополимеров. Спектры системы кристалл–адсорбированная молекула. Журнал прикладной спектроскопии, 1979, т. 30, № 3, с. 503-507.
3. D. Racovic, I. Bozovic, S.A. Stepanyan, L.A. Gribov. IR spectra and structure of poly(p–phenylene). A theoretical study. Solid State Communication, 1982, v. 43, No. 2, p. 127-129.
4. Л.А. Грибов, С.Д. Демухамедова, О.Б. Зубкова. Теоретический анализ и интерпретация колебательных спектров изотактического полимера. Поли–4–метил–пентен–1. Журнал прикладной спектроскопии, 1983, т. 38, № 2, с. 230-236.
5. Б.Л. Файфель, Л.А. Грибов. Расчет электронных состояний периодических структур методом РМХ. Журнал структурной химии, 1983, т. 24, № 3, с. 3-9.
6. D. Racovic, I. Bozovic, S.A. Stepanyan, L.A. Gribov. Theoretical study of infrared absorption in trans – (CH)x and trans – (CD)x. Physical Review B, 1983, v. 28, N 4, p. 1997-2000.
7. D. Racovic, I. Bozovic, L.A. Gribov, S.A. Stepanyan, V.A. Dementiev. Vibrational spectra of cis–(OH)x and cis–(OD)x: A theoretical study. Physical Review B, 1984, V. 29, № 6, p. 3412-3415.
8. L.A. Gribov, Ivan Bozovic, Dejan Racovic. Planar versus helical cis–polyacetylene. Physical Review B, 1985, V. 32, № 6, p. 4286-4288.
9. Л.А. Грибов, Л.И. Рейтблат. Новый метод уточнения частот и форм колебаний при расчете колебательных спектров полимеров. Журнал прикладной спектроскопии, 1987, т. 46, № 5, с. 766-772.
10. L.A. Gribov, B.K. Novosadov, O.Yu. Nikitin, L.I. Raitblat. An improved perturbation theory and its application to the spectral theory of polyatomic molecules. Journal of Molecular Structure, 1989, v. 188, p. 175-191.
11. Л.А. Грибов. Метод расчёта уровней энергии нанообъектов с периодической структурой скелета. Журнал структурной химии, 2010, Т. 51, № 1, С. 131-136.

A2e. Теория электронно-колебательных спектров [наверх]

Развиты методы прямого расчета колебательной структуры электронных спектров многоатомных молекул на основе адиабатической модели и специальных способах определения параметров молекулярных моделей в возбужденных состояниях. Решена проблемы вычисления всех матричных элементов теории (100 и более мерных интегралов), что обеспечивает возможность проведения расчетов без введения дополнительных приближений в теории.

Получены обобщенные выражения и расчетные формулы для преобразования нормальных координат комбинирующих электронных состояний, позволившие проводить реальные расчеты для сложных молекул как при малых, так и при больших (изомерных) их структурных перестройках при возбуждении.

Предложен и детально разработан вариационный метод решения колебательной задачи в возбужденных электронных состояниях, исключающий необходимость вычисления интегралов наложения колебательных волновых функций.

Предложены методы определения структурно-динамических параметров адиабатических моделей молекул в возбужденных состояниях (как геометрических, так и силовых).
Сформулирована физически корректная постановка обобщенной обратной электронно-колебательной задачи - задачи определения параметров адиабатических моделей молекул в возбужденных состояниях по их спектрам поглощения и флуоресценции.

Разработан метод, соответствующие алгоритмы и программы для ЭВМ для решения полной неадиабатической электронно-колебательной задачи, применимый для анализа крупных молекул и исключающий необходимость введения различных ограничений (случаи сильных и слабых вибронных взаимодействий, вырожденный случай, двухуровневая схема, одномодовое приближение и др.) сложных многоатомных молекул с большим числом близких по энергии состояний.

Предложена система "скрытых" молекулярных параметров адиабатических моделей, обеспечивающая возможность быстрого моделирования и предсказания спектральных свойств крупных молекулярных систем (до 100 и более атомов) и базирующаяся на ключевой в химии фрагментарной идее формирования молекулярных моделей для возбужденных состояний на основе данных, накопленных в соответствующих специализированных компьютерных банках.

Разработанные методы расчета электронно-колебательных состояний и спектров многоатомных молекул реализованы в виде комплекса программ для персональных компьютеров. Программный комплекс позволяет решать прямые и обратные задачи электронно-колебательной спектроскопии в их наиболее общем и корректном виде, а также проводить быстрое (в масштабе реального времени) моделирование молекул и их спектроструктурных свойств в видимой и УФ областях спектра.

Примеры расчета стационарных спектров приведены на рисунках.

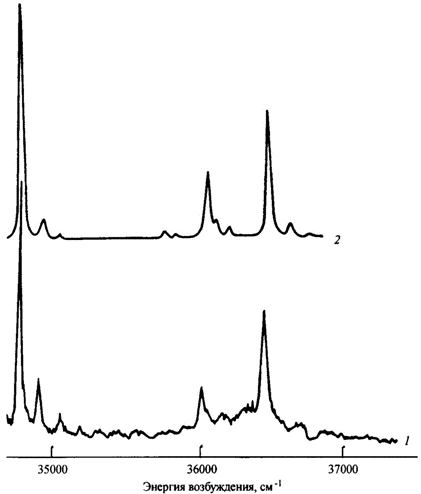
Экспериментальный (1) и рассчитанный (2) спектры возбуждения флуоресценции декатетраена

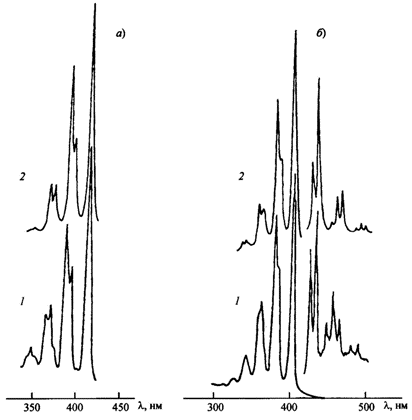
Экспериментальные (1) и рассчитанные (2) спектры поглощения гексадекагептаена (а) и тетрадекагептаена (б)

Развит метод расчёта тонкоструктурных электронно-колебательных спектров с временным разрешением («многомерных»).

Для моделирования многомерных спектров предложен подход, заключающийся в использовании для предсказания многомерных спектров параметрических молекулярных моделей (молекулярных фрагментов), построенных при расчете и анализе традиционных спектров поглощения и флуоресценции.

Разработаны эффективные методы решения систем кинетических уравнений большой размерности (N>10³), позволяющие проводить расчеты спектров и компьютерные эксперименты в масштабе реального времени.

Пример моделирования динамических спектров приведен на рисунке, где показаны результаты расчета полного спектра модели молекулы дифенилбутадиена при возбуждении всех колебательных подуровней состояния S₅ (а), его сечения при t = 0, 500, 1000, 2000 пс (б) и области, соответствующие различным электронным переходам (в, г, д).

1. Л.А. Грибов, В.И. Баранов, Б.К. Новосадов. Методы расчета электронно-колебательных спектров многоатомных молекул. Наука, Москва, 1984, 325 с
2. Л.А. Грибов, В.И. Баранов, Д.Ю. Зеленцов. Электронно-колебательные спектры многоатомных молекул. Теория и методы расчета. Наука, Москва, 1997, 475 с.
3. Л.А. Грибов, В.И. Баранов, М.Е.Эляшберг. Безэталонный молекулярный спектральный анализ. Теоретические основы. М.: Едиториал УРСС, 2002, 320 с. (глава 4)
4. Astakhov S.A., Baranov V.I., Gribov L.A. Theory and methods of computational vibronic spectroscopy. Hauppauge, NY: Nova Science Publishers, 2008, 87 p.

A3. Комплекс программ для ЭВМ [наверх]

Достаточное полное решение проблемы детального исследования сложных молекулярных систем подразумевает оперирование со многими моделями молекул и анализ большого числа характеристик. Следствием этого является переход от расчётных к исследовательским комплексам программ.

Этим требованиям удовлетворяет созданный программный комплекс LEV, который выполнен как составная часть исследовательской триады человек-компьютер-спектрометр.

Комплекс LEV позволяет решать на персональных компьютерах для молекул, содержащих сотни атомов, следующие задачи.

• Строить геометрические структуры многоатомных молекул и полимерных цепей поэлементно и с помощью соединения желаемым образом любых фрагментов, "вырезаемых" из полных молекулярных структур, имеющихся в специальном банке данных.
  
  
• Формировать потенциальную функцию методом автоматического поиска эквивалентных структурных элементов, методом фрагментарного заполнения соответствующей матрицы силовых постоянных с помощью банка данных, методом квантово-химического расчёта.
  
  
• Рассчитывать частоты и формы нормальных колебаний с возможностью демонстрации колебаний в виде движущихся мультипликационных изображений для молекул и полимерных цепей произвольной длины с учётом вклада концевых групп с автоматическим построением для полимеров частотных (дисперсионных) кривых и гистограмм.
  
  
• Рассчитывать кривые спектрального распределения коэффициентов поглощения и пропускания в колебательных спектрах сложных молекул и полимеров и значения интегральных оптических плотностей (абсолютных интенсивностей) в ИК спектрах молекул при любом заданном спектральном интервале и для нескольких интервалов.
  
  
• Решать задачи количественного анализа газов и жидкостей, в том числе смесей с небольшим числом компонент, без использования физических эталонов, а на основе вычисляемых характеристик (методом математического эталонирования).
  
  
• Вычислять квантово-химическими методами геометрию, силовые постоянные и электрооптические параметры (дипольные моменты связей и производные от них по колебательным координатам) для сложных молекулярных систем.
  
  
• Строить рельефные карты распределения электронной плотности и электростатического потенциала и электронно-ядерных сил в молекулах в заданных сечениях.
  
  
• Уточнять значения силовых постоянных и электрооптических параметров отдельных молекул или их совокупности средствами решения обратных спектральных задач с использованием штрафной функции.
  
  
• Строить потенциальные кривые при деформации молекулярной системы вдоль заданных направлений.
  
  
• Рассчитывать основные термодинамические функции молекулы.
  
  
• Анализировать факторы, влияющие на формирование наблюдаемых интенсивностей полос поглощения в ИК спектрах.
  
  
• Рассчитывать электронно-колебательные спектры заданных адиабатических моделей многоатомных молекул (как в кондоновском приближении, так и с учетом вибронного взаимодействия) и решать обратные электронно-колебательные задачи для поиска параметров этих моделей. Результатом является вычисление положений и интенсивностей линий колебательной структуры спектров, построение контуров электронно-колебательных полос и определение параметров адиабатических моделей молекул в возбужденных состояниях.
  
  
• Решать электронно-колебательные спектральные и структурные задачи для сложных молекул разработанным параметрическим полуэмпирическим методом вибронной спектроскопии с использованием новой системы «скрытых» молекулярных параметров для структурных молекулярных фрагментов, накопленных в соответствующих базах данных. Осуществлять моделирование спектров и поиск численных значений таких параметров для отсутствующих в базе фрагментов.
  
  
• Проводить расчеты динамических (с временным разрешением) вибронных спектров сложных молекул и их многокомпонентных смесей, ставить компьютерные эксперименты по исследованию влияния различных учитываемых факторов (например, спектральные и временные характеристики возбуждения) на вид таких спектров и получать информацию, необходимую для целенаправленного планирования постановки натурных экспериментов высокого и сверхвысокого разрешения (пико-, фемтосекундных).
  
  
• Решать вариационным методом полные неадиабатические задачи для сложных молекул в общем случае без введения различных ограничений (таких как, например, слабые и сильные вибронные взаимодействия, двухуровневое и одномодовое приближения и пр.). Проводить компьютерное моделирование неадиабатических эффектов и их анализ для реальных молекулярных структур.
  
  
• Моделировать на ПК фотохимические превращения сложных молекул. Строить временные зависимости заселенностей всех электронно-колебательных уровней многоизомерной молекулярной системы и полных трехмерных (частота, интенсивность, время) спектров поглощения и флуоресценции, а также любых их двумерных сечений, при любом (резонансном, широкополосном и др.) характере возбуждения системы. Вычислять квантовые выходы фотохимических реакций.

Комплекс LEV снабжен банком данных о геометрических, силовых и электрооптических параметрах многоатомных молекул (350 молекул) некоторых типичных органических классов. На основе этого банка можно за счёт комбинирования структурных элементов генерировать неограниченное число молекулярных моделей и их спектров.

С версией программ на языке Matlab, находящейся в стадии оформления, можно ознакомиться по адресу http://intranet.geokhi.ru/LevML/Домашняя.aspx

В лаборатории освоена техника параллельных вычислений и создана версия программ для компьютерного моделирования изомеризации и расчета динамических вибронных спектров сложных молекул на суперкомпьютере типа МВС 1000 (ИПМ РАН). Формирование задач, управление процессом вычислений и получение результата осуществляется дистанционно с ПК лаборатории.

1. Л.А. Грибов, В.А. Дементьев. Методы и алгоритмы вычислений в теории колебательных спектров молекул. Наука, Москва, 1981, 356 с.
2. В.И. Баранов, Ф.А. Савин, Л.А. Грибов Программы расчета электронно-колебательных спектров многоатомных молекул. - М.: Наука, 1983. - 192с.
3. Л.А. Грибов, В.А. Дементьев. Моделирование колебательных спектров сложных соединений на ЭВМ. Учебное пособие. Наука, Главн. ред физ-мат. лит., 1989, 158 с.

B. ЭКСПЕРТНЫЕ СИСТЕМЫ ДЛЯ УСТАНОВЛЕНИЯ СТРУКТУРЫ ОРГАНИЧЕСКИХ МОЛЕКУЛ [наверх]

В ноябре 2011 года издательством Королевского Химического Общества Великобритании выпущена в свет монография: M.E. Elyashberg, A.W. Williams, Blinov K.A. Contemporary Computer-Assisted Approaches to Molecular Structure Elucidation, Cambridge, RSC Publishing, 2012.

Книга, главным автором которой является ведущий научный сотрудник ГЕОХИ (по совместительству) проф. М.Е. Эляшберг, посвящена современным компьютерным методам установления структуры молекул по их спектрам.

Эта книга подводит итоги развития крупного научного направления, которое возникло в конце 60-х годов прошлого столетия. В международной научной литературе оно именуется как Computer-Assisted Structure Elucidation (CASE).

Первые работы по CASE были опубликованы одновременно группами Нобелевского лауреата Дж. Ледерберга (Стенфордский университет, США), Н. Мунка (Университет Аризоны, США), С. Сасаки (Университет Тохоку, Япония) и группой Л.А. Грибова (ГЕОХИ), в состав которой входил М.Е. Эляшберг. После появления этих работ в исследования включились многие ученые в разных странах мира. В этот период «штурма и натиска» были созданы теоретические основы компьютерного молекулярного спектрального анализа и разработаны многочисленные прототипы экспертных систем, моделирующих способ рассуждения специалиста при выявлении структуры по данным ИК, ЯМР и масс-спектрометрии. Возникла новая наука - математическая химия.

Группой Л.А. Грибова внесен значительный вклад в создание, становление и дальнейшее развитие этого нового научного направления, которое впитало в себя достижения целого ряда научных дисциплин – экспериментальной и теоретической спектроскопии, органической химии, математической логики, теории графов, комбинаторики, теории вероятностей и т.д.

В ГЕОХИ была предложена и теоретически обоснована общая архитектура экспертной системы (ЭС), предназначенной для распознавания структуры молекул по их спектрам, и разработаны математические алгоритмы, обеспечивающие ее программную реализацию.

На базе дискретной модели системы молекула-спектр была разработана математическая теория структурно-группового анализа (СГА) сложных органических молекул по их спектрами и было показано, что логическая задача СГА имеет алгоритмическое решение в терминах булевой алгебры.

Оказалось, что общий ход рассуждений специалиста при выполнении СГА может быть описан в терминах логических уравнений. Установлен общий вид основного логического уравнения СГА и предложен алгоритм его решения, дающего все наборы фрагментов, которые удовлетворяют исходным данным. В ходе дальнейших исследований были разработаны теория и алгоритмы генерации структурных формул из атомов и фрагментов на базе теории графов и комбинаторики. На примере ИК спектроскопии было показано, что наиболее вероятная структура может быть выявлена на основании предсказания колебательных спектров сгенерированных структур.

Важную роль в развитии теории экспертных систем сыграли работы группы Л.А. Грибова, в которых была исследована природа и структура знаний, используемых для определения структуры.

Показано, что выявление знаний, необходимых для установления структуры данной молекулы по ее спектрам, эквивалентно построению частной аксиоматической теории, а генерация структур позволяет найти все без исключения следствия из этой теории. Наиболее значимое следствие находится в результате предсказания спектров предполагаемых структур.

Разработаны принципы формирования базы знаний экспертной системы, куда включаются фактические и аксиоматические знания. Частная аксиоматическая теория в каждом конкретном случае формируется автоматически на основании совместного анализа информации, содержащейся в базе знаний и экспериментальных спектрах неизвестного вещества.

Решение перечисленных выше задач явилось существенным вкладом в создание математической химии и, в частности, математической аналитической химии.

Предложенная архитектура ЭС очерчивает основные блоки, которые должна содержать любая система, предназначенная для установления структуры молекул по их спектрам. Практика показала, что по мере развития науки, блоки, образующие систему, усовершенствуются и даже меняются принципы их построения, но архитектура системы остается в рамках описанной схемы.

На базе развитых теоретических подходов в группе Л.А. Грибова было разработано несколько поколений экспертной системы РАСТР. В результате дальнейшего развития алгоритмов системы РАСТР, М.Е. Эляшбергом совместно с фирмой Брукер (ФРГ) была создана экспертная система X-PERT, базирующаяся на использовании ¹³С и ¹Н ЯМР, ИК и масс-спектров, в которой в высокой степени реализована идея симбиоза исследователя и компьютера. Программа была включена в стандартное математическое обеспечение ЯМР и ИК спектрометров фирмы БРУКЕР.

Следует отметить, что история нового научного направления не была лишена драматизма. К концу 80-х годов стало очевидно, что количество структурной информации, извлекаемой из ИК, ЯМР и масс-спектров, не достаточно для установления структуры крупных молекул природных соединений. Это обстоятельство породило глубокое разочарование. Исследования по развитию экспертных систем в мире перестали поддерживаться грантами, и большинство ученых прекратили исследования в этой области. По образному выражению Курта Вармузы, работу продолжили только бойцы, сражающиеся с ветряными мельницами. Поскольку М.Е. Эляшберг с самого начала работал по данной тематике на одном энтузиазме и без какой-либо финансовой поддержки, то для него ничего не изменилось, и он, не потеряв веру в успех, продолжал упорно сражаться... В 90-х годах стали доступными двумерные (2М) ЯМР спектры, несущие богатую структурную информацию, необходимую для идентификации крупных молекул. Это обстоятельство не только вывело CASE из кризиса, но и привело экспертные системы к крупным успехам.

В Московском отделе канадской научной фирмы Advance Chemistry Development (ACD), куда М.Е. Эляшберг был приглашен на работу, удалось разработать экспертную систему Structure Elucidator (StrucEluc), предназначенную для установления структуры крупных органических молекул (более 100 скелетных атомов) по 1М (¹³С, ¹Н) и 2М ЯМР, ИК и масс-спектрам. Система позволяет выявлять структурную формулу неизвестного соединения, определять его стереоконфигурацию и строить трехмерную модель. С помощью системы StrucEluc, которая теперь широко используется во всем мире (приобретена более чем 100 организациями), установлены структуры тысяч впервые выделенных или синтезированных соединений. Она применяется в таких крупных компаниях, как Pfizer, Novartis, Merck, Roche, AstraZeneca, Bayer, Mitsubishi, Shell, Samsung, а также во многих университетах Америки, Европы и Азии. В 2011 г. началось ее применение и в России...

Таким образом, можно говорить, что в результате развития идей и методов CASE удалось полностью формализовать задачу установления структуры нового органического соединения, что позволило создать мощный и гибкий инструмент молекулярного спектрального анализа.

Примеры молекул природных соединений, структура которых была установлена с помощью StrucEluc, показаны ниже:

Развитие СASE можно проследить по следующим работам:

1. L.A. Gribov, M.E. Elyashberg. Computer-aided identification of organic molecules by their molecular spectra, (A Monographic Review). Critical reviews in analytical chemistry, 1979, v. 8, N 2, p. 111-220.
2. М.Е. Эляшберг, Л.А. Грибов, В.В. Серов. Молекулярный спектральный анализ и ЭВМ. Москва, Наука, 1980. 307 с.
3. Л.А. Грибов, В.И. Баранов, М.Е. Эляшберг. Безэталонный молекулярный спектральный анализ. Теоретические основы. Москва, УРСС, 2002. 317 с.
4. M.E. Elyashberg, K.A. Blinov, S.G. Molodtsov, A.J. Williams, G.E. Martin. Structure Elucidator: A Versatile Expert System for Molecular Structure Elucidation from 1D and 2D NMR Data and Molecular Fragments. J. Chem. Inf. Comput. Sci., 2004, v. 44, p. 771-792.
5. M.E. Elyashberg, A.J. Williams, G.E. Martin. Computer-Assisted Structure Verification and Elucidation Tools in NMR-Based Structure Elucidation (Monographic Review). Progress in NMR spectroscopy, 2008, v. 53, N 1/2, p. 1-104.
6. M.E. Elyashberg, A.W. Williams, Blinov K.A. Contemporary Computer-Assisted Approaches to Molecular Structure Elucidation, Cambridge, RSC Publishing, 2012

C. ТЕОРИЯ МОЛЕКУЛЯРНЫХ ПРОЦЕССОВ [наверх]

C1. Структурные превращения (химические реакции) [наверх]

Предложена последовательная квантовая теория химических реакций в крупных молекулах, основанная на представлении о безызлучательных резонансных переходах между стационарными состояниями структурных изомеров (мономолекулярные реакции структурной изомеризации) и квазистационарными слабо связанными комплексами (реакции синтеза и разложения) при сохранении общего атомного состава. Математически ход реакции описывается миграцией волнового пакета от исходного состояния к результирующему. Подход базируется на общих принципах квантовой механики и позволил с единых позиций описать механизмы различных реакций и объяснить некоторые общие закономерности.

Химические реакции трактуются как результат превращения исходной геометрической конфигурации молекулярной системы в другую структуру объекта при перестановке атомов. В реакциях структурной изомеризации атомы в новых положениях оказываются прочно связанными между собой. В реакциях синтеза исходные слабые межмолекулярные связи заменяются на достаточно прочные химические. В реакциях разложения перестановки атомов приводят, наоборот, к сильному ослаблению некоторых химических связей и появлению пары слабо связанных молекулярных объектов.

Подобные превращения соответствуют переходам из одного допустимого стационарного или квазистационарного состояния системы в другое. Для этого необходимо, во-первых, чтобы между этими состояниями существовала связь, и, во-вторых, чтобы при наличии такой связи волновая функция исходного состояния максимально смешивалась с функцией другого. Это возможно, если комбинирующие функции отвечают одинаковым по энергии состояниям системы. В этом случае возникает резонанс и полное смешивание происходит при любом отличном от нуля матричном элементе взаимодействия. Переход совершается без изменения энергии. Время перехода зависит от величины матричного элемента. Это позволяет ввести понятие вероятности химической реакции и охарактеризовать кинетику процесса.

Математическая модель явления базируется на энергетической (гамильтоновой) матрице в базисе, отвечающем электронно-колебательным состояниям взаимопревращающихся молекулярных структур. Энергетическая матрица строится аналогично матрице в базисе АО в квантовой химии, но с вариационной функцией в форме линейной комбинации функций изомеров (ЛКФИ), где роль АО будут играть электронно-колебательные функции отдельных учитываемых при постановке задачи молекулярных структур. При этом расположение АО в декартовом пространстве заменяется расположением функций изомеров в пространстве внутренних (нормальных) координат. Это расположение по отношению к исходному изомеру легко задать, пользуясь найденными матричными соотношениями Q_k = A_kQ₁ + b_k, где индекс k маркирует изомеры. Ниже дано сравнение схем построения модельной матрицы H в квантовой химии и методе ЛКФИ.

Развитие процесса во времени описывается зависящим от времени уравнением Шредингера с постоянной энергетической матрицей.

Если имеются два (в простейшем случае) стабильных резонирующих состояния, причём в начальной момент заселяется одно из них, и если между состояниями с функциями ψ₁ и ψ₂ имеется взаимодействие, то при резонансе уровней возникают квантовые биения с волновой функцией, квадрат которой равен

где ω = 2ħ^-1h_nk. Получается волновой пакет, мигрирующий с частотой ω.

Требование резонанса состояний (уровней) подсистем является условием необходимым для хода реакции, но не достаточным. Для того чтобы реакция произошла, необходимо, чтобы функции ψ₁ и ψ₂ имели заметную область перекрывания, которая характеризуется соответствующим интегралом. Показано, что вероятность реакционного перехода пропорциональна величине exp(-b²), где b² - квадрат модуля сдвига нормальных координат. Это позволяет сразу, не прибегая к сложным вычислениям, разделить все реакции на быстрые и медленные. Матрицы A и векторы b легко вычисляются для молекул любой сложности. В результате можно ранжировать по вероятности возможные пути химических превращений (см. пример на рисунке) и ввести понятие матрицы смежности для любых возможных химических реакций, отвечающих продуктам превращения исходного молекулярного объекта.

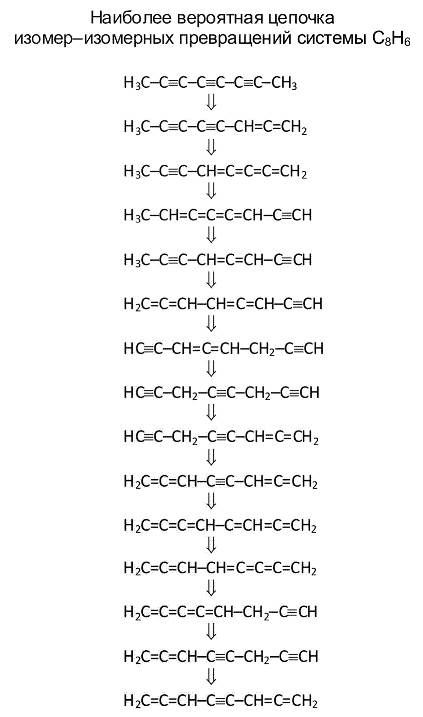
На основании предложенной теории удалось, опираясь лишь на первые принципы, получить большое число выводов, целиком совпадающих с общими закономерностями хода химических реакций в сложных молекулах, обнаруженными в химии, в частности:

• Необходимость реакционных центров (указан и метод их поиска с помощью выявления характеристических по форме колебаний)
  
  
• Закон Аррениуса
  
  
• Эффект появления индукционной стадии реакции и S-образный вид зависимости скорости реакции от времени
  
  
• Возможность появления безэнергетических низкотемпературных периодических реакций Белоусова-Жаботинского
  
  
• Особенности протекания реакций при повышенных температурах и очень низких (криохимия)
  
  
• Различия в механизмах реакций с участием малых и сложных молекул;
  
  
• Механизм кинетического изотопного эффекта, роль переноса атома водорода при реакциях в органических молекулах и др.
  
  

Указано на существование нового типа движения, характерного для крупных молекулярных объектов – перенос энергии, заряда и сигнала при последовательной структурной изомеризации.

Решен ряд базовых вопросов, связанных с приемом и преобразованием информации в молекулярном мире: запись сигнала, распознавание образа, обучение и др. Тем самым заложены теоретические основы важного научного направления - молекулярной логики.
Результаты обобщены в монографии.

1. Л.А. Грибов, В.И. Баранов. Теория и методы расчета молекулярных процессов: спектры, химические превращения и молекулярная логика. М: «КомКнига», 2006, 480 с.

C2. Фотохимия [наверх]

На основании ранее разработанной общей квантовой теории химических реакций впервые поставлена и решена задача об оценке квантовых выходов фотохимических реакций.

C2a. Априорные количественные предсказания квантовых выходов фотохимических реакций [наверх]

Показана возможность проведения предсказательных расчетов кинетики и квантовых выходов фотохимических превращений сложных молекул с удовлетворительной точностью прогноза. С учетом наложенных физически обоснованных требований и достаточно жестких ограничений на погрешность предсказания (менее 50%) для всех рассмотренных реакций, относящихся к трем химически разным типам, достигается удовлетворительный теоретический результат. В большинстве случаев (8 из 10 реакций) отклонение от эксперимента менее 20%.

Параметры модели обладают высокой степенью переносимости в ряду однотипных реакций, что обеспечивает предсказательный характер моделирования фотохимических процессов развитым методом. В сложных случаях можно априори теоретически оценивать, к какому типу относится рассматриваемая реакция и ее физико-химические особенности.

C2b. Модельный подход и результаты расчетов [наверх]

Предложен полуэмпирический подход, опирающийся на основные физические принципы построения всех работоспособных физических теорий в спектроскопии и квантовой химии.

В основе предлагаемого метода моделирования фотохимических процессов лежат следующие положения: (1) превращение исходной структуры в конечную трактуется как безызлучательный переход из одной потенциальной ямы в другую, отделенную от первой барьером; (2) переход считается возможным при возникновении резонанса между состояниями комбинирующих структур, имеющими близкие энергии; (3) вероятность перехода определяется величиной интеграла перекрывания волновых функций комбинирующих состояний. Для учёта асимметрии потенциальных ям, обусловленной наличием барьера, используются эмпирические параметры, задающие величину «уширения» ям вдоль всех или части нормальных координат. Выяснено, что наиболее эффективной функцией уширения является ступенчатая. Показана возможность проведения предложенным методом прогностических расчетов фотохимических превращений и квантовых выходов реакций с погрешностью (отклонение от эксперимента) порядка и менее 50%.

Результаты выполненных расчетов фотоизомеризации ряда молекул (более 15 реакций) показали перспективность развиваемого метода, так как обеспечивается количественное прогнозирование квантовых выходов реакций на хорошем уровне согласия с имеющимися экспериментальными данными (см. таблицу).

Для реально наблюдаемых реакций с квантовыми выходами в пределах 0.01–1 отклонение прогнозируемых значений от экспериментальных составило 10–50 %. В тех случаях, когда по экспериментальным данным реакции не идут, рассчитанные значения квантовых выходов также оказываются пренебрежимо малыми - менее 10^-9. Количественно верно предсказывается и соотношение величин квантовых выходов рассмотренных фотопревращений молекул, включая и случай аналогичных фотохимических процессов с качественно (на порядки величин) различающимися значениями квантовых выходов.

Установлено, что при выполнении условия относительной малости вероятностей оптических переходов по сравнению с частотой квантовых биений количественные оценки квантовых выходов с удовлетворительной степенью точности могут быть получены непосредственно по величинам вероятностей переходов без проведения полного расчета кинетики фотопревращения.

Выявлена причина наблюдающегося в эксперименте существенного различия квантовых выходов однотипных реакций для сходных молекул, но при разных заместителях. Она заключается в изменении форм колебаний при структурной перестройке, когда заместитель непосредственно в ней участвует. Показана высокая чувствительность интегральных характеристик фотохимических реакций (квантовых выходов) к конформации участвующих в процессе молекул.

Поставлена и решена задача о ходе фотохимических реакций при наличии произвольного числа квазирезонирующих уровней энергии комбинирующих подсистем. Такая многоуровневая ситуация наиболее характерна для крупных молекул с высокой плотностью распределения электронно-колебательных возбужденных уровней энергии. Это приводит, в частности, к появлению ветвления путей фотохимических превращений. Показано, что и в таком общем случае (как и в рассмотренном ранее частном для двукратного квазивырождения) можно ввести объединенный уровень энергии для исходной молекулы и продуктов ее фотохимических превращений и сформировать волновой пакет, позволяющий описать кинетику процесса. Результат иллюстрируется таблицей.

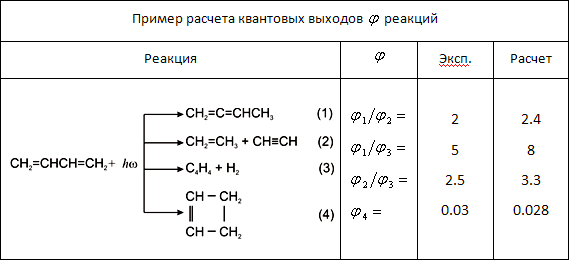
Полученные общие выражения позволяют проводить детальное моделирование процесса фотоиндуцированного превращения для молекул любой степени сложности и при произвольных условиях оптического возбуждения. Как и в простом двухуровневом случае, поведение во времени волнового пакета взаимодействующих возбужденных электронно-колебательных состояний молекулярной системы носит характер миграции возбуждения между состояниями комбинирующих подсистем. Отличительной особенностью является сложный характер квантовых биений, возникающих уже при относительно небольшом числе квазивырожденных уровней. Миграция волнового пакета носит ярко выраженный непериодический характер, однако временная характеристика процесса структурного превращения относительно мало меняется при квантовых биениях. Такая особенность позволяет свести задачу к двухуровней модели с усредненным значением времени перехода.

Недостаток этого модельного подхода состоит в том, что при учете ангармонизма потенциальных функций (асимметрии ям) применялся наиболее простой из возможных вариантов, заключающийся в использовании гармонических колебательных функций, получаемых при уширении потенциальных ям, одинаковом по всем нормальным координатам. Этот недостаток был преодолен. Разработана модель с дифференциальным по нормальным координатам учетом асимметрии потенциальной функции.

Показана эффективность этой модели и возможность проведения предсказательных расчетов кинетики и квантовых выходов фотохимических превращений сложных молекул с удовлетворительной точностью прогноза.

Выяснено, что данная модель адекватно отражает особенности структурных превращений многоатомных молекул, при которых, как было показано ранее (Грибов Л.А., Баранов В.И. Теория и методы расчета молекулярных процессов: спектры, химические превращения и молекулярная логика. М.: КомКнига, 2006), преобразуется относительно малое число координат из их общего количества. С учетом наложенных физически обоснованных требований и достаточно жестких ограничений на погрешность предсказания (менее 50%) для всех рассмотренных реакций достигается удовлетворительный теоретический результат. В большинстве случаев (8 из 10 реакций) отклонение от эксперимента менее 20%.

Параметры модели обладают высокой степенью переносимости в ряду однотипных реакций, что обеспечивает предсказательный характер моделирования фотохимических процессов развитым методом. В сложных случаях можно априори теоретически оценивать, к какому типу относится рассматриваемая реакция и ее физико-химические особенности, поскольку значения параметров модели U₀ и X₀ для реакций разных типов лежат в областях, существенно разнесенных в пространстве (U₀,X₀). Это проиллюстрировано ниже на рисунке.

Области значений параметров модели U₀, X₀, для реакций типов I, II и III, отвечающие теоретическим значениям квантовых выходов, отклоняющимся от экспериментальных не более чем на 50%.
Точки (•) соответствуют оптимальным значениям параметров U₀, X₀ для групп реакций.

На основе общей теории молекулярных превращений можно утверждать, что физическая природа и теоретическая модель процесса химического превращения молекул не зависит от характера его инициации – например, оптического или теплового возбуждения. Поэтому по результатам фотохимического эксперимента, наиболее вариабельного по его постановке и информативного по результатам, можно получить данные о молекулярной модели, необходимые для оценки времени и кинетики термических реакций.

1. В.И. Баранов, Л.А. Грибов, В.Е. Дридгер, И.Х. Исхаков, И.В. Михайлов. Метод моделирования фотохимических процессов и расчёта квантовых выходов реакций. Химия высоких энергий, 2009, т. 43, № 5, с. 416-423
2. В.И. Баранов, Л.А. Грибов, В.Е. Дридгер, И.Х. Исхаков, И.В. Михайлов. Моделирование фотохимических процессов и расчёт квантовых выходов реакций изомеризации замещённых диенов. Химия высоких энергий, 2009, т. 43, № 6, с. 545-551
3. В.И. Баранов, Л.А. Грибов, В.Е. Дридгер, И.В. Михайлов. Расчёт квантового выхода реакции изомеризации метоксибута диен-метоксициклобутан. Химия высоких энергий, 2010, т. 44, № 3, с. 209-212
4. В.И. Баранов, Л.А. Грибов, М.Х. Исхаков, И.В. Михайлов. Моделирование процессов фотоизомеризации циклопропилкарбоксальдегида и расчёт квантового выхода реакций. Химия высоких энергий, 2010, т. 44, № 4, с. 307-312
5. Л.А. Грибов, В.И. Баранов. Теория разветвлённых бифуркационных фотохимических реакций. Химия высоких энергий, 2010, Т. 44, № 6, С. 496-505
6. Baranov V.I., Mikhailov I.V., Poteshnaya N.I. Optimization of molecular models for calculating quantum yields of photochemical reactions. In book: Chemical and Biochemical Technology. Materials, Processing, and Reliability (editor: Varfolomeev S.D. New Jersey: Apple Academic Press. 2014. 380 p.) P. 35-54 (chapter 3).
7. Баранов В.И., Грибов Л.А., Михайлов И.В., Потешная Н.И. Модифицированный метод расчета квантовых выходов фотохимических реакций. Химия высоких энергий. 2014. Т. 48. № 1. С. 49-56
8. Баранов В.И., Грибов Л.А., Михайлов И.В., Потешная Н.И. О возможности априорных количественных предсказаний квантовых выходов фотохимических реакций. Химия высоких энергий. 2015. т. 49. № 2. С. 103-111.

C3. Механохимия [наверх]

Предложена теория механохимических процессов как результата перестановки атомов, стимулированной накоплением энергии при интерференции волн, возникающих в реакционных центрах крупных молекулярных и нанообъектов после краевых механических возмущений.

Задача сведена к решению зависящих от времени уравнений о колебаниях молекулярных структур произвольного строения и размеров с заданными начальными условиями. Возникает возможность связать описываемые средствами молекулярной динамики процессы с внутримолекулярными.

Теория позволяет использовать все предложенные ранее в общей теории колебаний молекул системы координат, вычислительные алгоритмы и совокупности молекулярных параметров (силовые постоянные). Ограничений на размеры изучаемых объектов, характеры возмущений и типы структур нет.

1. Л.А. Грибов, Н.И. Прокофьева. Волновые движения атомов в молекулярных наноструктурах. Журнал структурной химии, 2008, т. 49, № 4, с. 723-727.
2. Л.А. Грибов, В.А. Дементьев. Волновые движения в молекулярных наноструктурах: результаты компьютерных экспериментов. Журнал структурной химии, 2010. Т. 51. № 2. С. 331-336.

D. МАТЕМАТИЧЕСКИЕ ПРОБЛЕМЫ [наверх]

D1. Теория многомерных гипергеометрических функций [наверх]

Теория многомерных гипергеометрических функций или рядов до 1980 г. представляла собой слабо упорядоченное знание по огромному многообразию математического анализа этих рядов.

Найденный и примененный метод факторизации гипергеометрических рядов позволил существенно упорядочить классификацию данных функций и исследовать аналитические свойства многомерных гипергеометрических рядов.

Появился мощный алгебраический аппарат воспроизведения данных рядов с помощью дифференцирований простейших гипергеометрических функций. Тем самым гипергеометрические ряды могут быть получены и классифицированы с помощью машинной аналитики, избавляя исследователя от утомительной работы по доказательству тождественности какого-либо гипергеометрического ряда уже известному в литературе представителю класса гипергеометрических рядов.

Метод факторизации гипергеометрических рядов получил одобрение и высокую оценку крупнейшего математика XX века И.М. Гельфанда.

1. Ниукканен А.В. Новый метод в теории гипергеометрических рядов и специальных функций математической физики. Успехи матем. наук, 43:3 (1988), 191-192.
2. Ниукканен А.В. Общие линейные преобразования гипергеометрических функций, Матем. заметки, 70:5 (2001), 769-779.

D2. Теория возмущений [наверх]

Показано, что ряд теории возмущений Релея-Шредингера получается как следствие метода вращений Якоби при малых углах вращения.

Предложена формула, позволяющая вычислять поправки к значениям отдельных уровней энергии в случае вырождений и квазивырождений.

1. L.A. Gribov, B.K. Novosadov, O.Yu. Nikitin, L.I. Raitblat. An improved perturbation theory and its application to the spectral theory of polyatomic molecules. Journal of Molecular Structure, 1989, v. 188, p. 175-191.

E. ТЕОРЕТИЧЕСКАЯ АНАЛИТИКА [наверх]

E1. Безэталонный молекулярный спектральный анализ [наверх]

Предложено использовать возможности численных расчётов наблюдаемых в экспериментальных спектрах молекул характеристик (положения линий и полос на шкале длин волн или волновых чисел, их интенсивности и временные изменения при импульсных воздействиях) для решения качественных и количественных аналитических задач при анализе индивидуальных соединений и их смесей.

Развита теория таких анализов по спектрам разной природы.

В целом аналитическая задача решается полностью, причём исключается необходимость использования образцов стандартного состава (эталонов) и резко повышается степень универсальности методов оптической молекулярной спектроскопии. Появляется возможность априорного, исходя из поставленной проблемы, планирования эксперимента и отбора необходимых для этого измерительных средств.

E1a. Сравнение теоретических и экспериментальных спектральных кривых [наверх]

Показано, что сравнение теоретических и экспериментальных спектральных кривых требует учёта влияния измерительного прибора (спектрометра) и, поэтому, выполнения операции редукции идеального спектра к реальному (наблюдаемому). Сопоставление экспериментальных спектров и теоретических после такой редукции производится и по форме спектральных кривых, и по интегральным интенсивностям поглощения или излучения энергии в широких спектральных интервалах.

Неизбежные погрешности эксперимента и несовпадения теоретических спектров с Природой, а также влияние межмолекулярных взаимодействий учитываются с помощью статистических имитаций и перехода к нечётким множествам. Впервые указано, что нечёткий спектр любого происхождения можно описать с помощью прямоугольных матриц, содержащих информацию как о случайных, так и о систематических погрешностях.

E1b. Определение абсолютных концентраций в смеси веществ по спектральным данным без использования образцов стандартного состава (эталонов) [наверх]

Предложено общее матричное уравнение для проведения качественного и количественного анализов чистых веществ и смесей по измеренным спектрам сумм компонент. Сформулирован алгоритм решения уравнения, позволяющий априори автоматически оценить степень достоверности найденных величин (концентраций). Ответ получается в абсолютной шкале: число поглощающих или излучающих частиц в единице объёма.

Доказано, что процесс поиска решения всегда сходится и отвечает критерию наименьших квадратов. Алгоритм может быть применён к спектрам любого происхождения: стационарные ИК и КР спектры, люминесценция, зависящие от времени и др., к любым их сочетаниям и при произвольных методах возбуждения.

E1c. Общая постановка задачи анализа вещества по продуктам фотохимических реакций [наверх]

Целью исследования являлось постановка задачи и разработка формальной процедуры установления структуры и определения количества вещества по продуктам его фотохимической реакции. Такая проблема возникает при исследованиях быстропротекающих фотохимических процессов, когда время жизни исходного вещества меньше интервала времени до момента его регистрации (экология, отравляющие вещества и др.).

Рассмотрены алгоритмы решения соответствующих обратных задач и предложена процедура, состоящая из нескольких шагов: (1) по спектральным данным для исследуемого образца с помощью теории молекулярных спектров определяется состав и концентрации компонентов смеси; (2) по структурным формулам продуктов химической реакции восстанавливается качественный состав исходного вещества; (3) на основе развитой теории химических превращений с использованием информации о реагирующих веществах и их концентрациях определяются начальные концентрации и кинетика процесса.

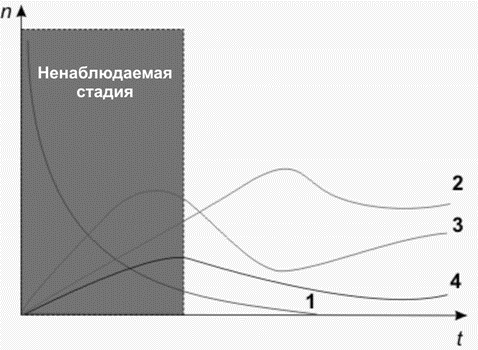
Изменение во времени количества исходного вещества (1) и продуктов реакции (2,3,4)

E1d. Принципы безэталонного молекулярного спектрального анализа смесей в условиях фотохимических превращений молекул [наверх]

Сформулирована постановка задачи и разработана формальная процедура безэталонного молекулярного спектрального анализа многокомпонентных смесей с учетом протекающих в них фотохимических превращений молекул.

Рассмотрен случай, когда временная зависимость спектра смеси определяется только изменением во времени концентраций компонентов, а спектры индивидуальных компонентов остаются постоянными. Выявлены соответствующие требования к физико-химическим свойствам молекул и показано, что они удовлетворяются для весьма широкого круга многоатомных молекул и протекающих реакций. Исключением являются молекулы с метастабильными возбужденными электронными состояниями.

Большая серия проведенных модельных расчетов, отвечающих реальным молекулярным структурам и экспериментально наблюдаемым их фотохимическим превращениям, показала работоспособность предлагаемого подхода. Решение задачи сходится к точным значениям и устойчиво к погрешностям задания исходных спектральных данных, обусловленных особенностями проведения эксперимента, выбора теоретических моделей и др. факторами.

Получаемые теоретические значения концентраций отвечают критерию наименьших квадратов, а их погрешности оцениваются по величине дисперсии на единицу веса. Дисперсия позволяет оценить уровень шума в используемых в анализе спектральных данных, достоверность получаемого результата и может служить критерием корректности исходной гипотезы о качественном составе многокомпонентной смеси.

Зависимость величины дисперсии D^1/2 получаемого решения аналитической задачи от уровня шума δ_S в используемых спектральных данных

E1e. Комбинированный ИК-УФ-фотохимический метод безэталонного анализа [наверх]

Теоретически обоснована возможность построения комбинированного ИК-УФ-фотохимического метода безэталонного спектрального анализа смеси близких по структуре и оптическим свойствам изомеров. Предложен возможный способ проведения такого анализа.

Схема проведения эксперимента

Необходимым условием натурной постановки и реализации метода является проведение компьютерных экспериментов, базирующихся на теории и методах расчета ИК и электронно-колебательных спектров, кинетики и квантовых выходов фотохимических реакций.

Показана эффективность включения в методику анализа процессов фотохимических превращений молекул. По возникающим временным зависимостям спектров можно интерпретировать их, определив наличие разных компонент в смеси и их количество и выделив отвечающие им спектральные составляющие в суммарном спектре. Это дает возможность на следующем этапе использовать развитые стандартные методы качественного и количественного безэталонных анализов.

E1f. Степенные полиномы и задача количественного анализа смесей [наверх]

Рассмотрен вопрос о разделении аддитивных спектров смесей известного качественного состава на составляющие. Предложен алгоритм нахождения концентраций компонентов таких смесей, основанный на представлении спектральных кривых произвольной природы степенными полиномами. Алгоритм предусматривает поиск решения в условиях нечётких множеств, характеризующих исходную информацию о спектрах компонентов. Работоспособность подхода проверена с помощью большой серии компьютерных экспериментов на примере ИК спектров пятикомпонентных смесей органических веществ.

Гистограммы распределения концентраций пяти компонентов смеси (1) транс-1,2-дифенилэтилена,
(6) пентаметилпиридина, (10) циклогексилциклогексана, (13) гексана и (20) 1,8-нонадиина
при 25%-ых вариациях значений волновых чисел и интенсивностей спектров.
Заданные концентрации компонентов 1.0, 2.5, 5.0, 7.5 и 10.0 соответственно

1. Грибов Л.А., Баранов В.И., Эляшберг М.Е. Безэталонный молекулярный спектральный анализ. Теоретические основы. Изд. Эдиториал УРСС, Москва, 2002, 317 с.
2. Astakhov S.A., Baranov V.I., Gribov L.A. Standardless spectrochemical analysis and direct simulations of time-resolved vibronic spectra of polyatomic molecules isomers and mixtures. Journal of Molecular Structure, 2003, v. 655, p. 97-123.
3. Грибов Л.А. Теоретическая физика – аналитике. Журнал аналитической химии, 2011. Т. 66. № 3. С. 247-268.
4. Монахова Ю.Б., Астахов С.А., Муштакова С.П., Грибов Л.А. Методы декомпозиции спектров различной природы в анализе смесей сложного состава. Журнал аналитической химии. 2011. Т. 66. № 4. С. 361-372.
5. Баранов В.И., Грибов Л.А., Дридгер В.Е. Компьютерное моделирование безэталонного спектрального анализа смесей. Журнал аналитической химии. 2012. Т. 67. № 2. С. 150-158.
6. Баранов В.И., Грибов Л.А., Исхаков М.Х. Общая постановка задачи анализа вещества по продуктам фотохимических реакций. Журнал аналитической химии, 2012. Т. 67. № 3. С. 236-244.
7. Грибов Л.А., Михайлов И.В., Прокофьева Н.И. Степенные полиномы и задача количественного анализа смесей. Журнал аналитической химии. 2015. Т. 70. № 9. С. 933-947.
8. Баранов В.И., Грибов Л.А., Михайлов И.В. О возможности безэталонного молекулярного спектрального анализа смесей в условиях фотохимических превращений молекул. Химия высоких энергий. 2016. Т. 50. № 5. С. 335–344.

E2. Влияние полярных заместителей [наверх]

Выполнена серия исследований о влиянии удалённых от реакционного центра полярных заместителей на ход ион-молекулярных реакций и прочность образующих координационных соединений и Н-связей.

Показано, что полярный заместитель может сильно изменить характер распределения электронной плотности непосредственно в своей окрестности в радиусе не более трёх-четырёх ангстрем. Изменения электронной плотности на больших расстояниях малы и практически не оказывают влияния на свойства реакционного центра. Наблюдающиеся изменения хода реакций и прочности образующихся координационных или Н-связей при введении в молекулу полярных заместителей объясняются не вариациями собственно электронной плотности, а часто довольно сильными изменениями характера и напряжённости внешнего молекулярного электростатического поля молекулы в месте расположения металла при образовании координационной связи и атома Н при образовании межмолекулярной Н-связи. Корреляция прочности таких связей и потенциала внешнего электростатического молекулярного поля оказывается близкой к линейной.

1. L.A. Gribov, S.B. Savvin. The mechanism of the distant substituent effect on molecule reactivity. Journal of Molecular Structure, 1981, v. 71, p. 263-278.
2. Л.А. Грибов, С.П. Муштакова. Квантовая химия. Учебник - М.: Гардарики, 1999, 390 с.

E3. Хроматографический эффект в колонке с периодически изменяющимся поперечным
сечением. Теоретический анализ [наверх]

Теоретически рассмотрена возможность использования колонки с периодически изменяющейся площадью поперечного сечения в жидкостной хроматографии. Предложена базовая физическая модель движения частицы в ламинарном потоке элюента по такой колонке. Показано, что проявление хроматографического эффекта разделения компонентов является следствием различия средних по времени скоростей движения. Возможно использование трубок с периодически меняющейся площадью поперечного сечения в качестве хроматографических колонок совершенно нового типа.

Зависимости абсолютного значения расстояния между двумя частицами (m/A = 1 и 0.2) от времени при разных значениях пространственного периода трубки ω, т.е. протяжённости узких и широких участков: ω = 1 (1), 0.4 (2), 0.2 (3). A – константа, зависящая от вязкости жидкости и поперечного сечения частицы и не зависящая от её массы m.

F. ПРОЧИЕ ИССЛЕДОВАНИЯ [наверх]

F1. Общая методология исследования микромира [наверх]

С позиций принципа дополнительности Бора проанализирована общая методология исследования микромира, в частности крупных молекул и полимеров, косвенными физическими методами (спектроскопия, электронная дифракция и др.).

Показано, что следствием этого принципа является необходимость для достижения "ясности" пользоваться различными модельными представлениями молекулярных систем (структурные формулы, жесткие пространственные модели, модели, допускающие упругие деформации и внутреннее вращение и др., модели с зарядовым распределением и т.д.). Неполное соответствие этих моделей реальным природным объектам приводит к необходимости постановки и решения разного рода обратных задач, переходу к полуэмпирическим теориям и появлению элементов субъективизма в окончательных результатах.

Описывающие различные свойства крупных молекулярных систем теории и методы расчётов могут быть только полуэмпирическими и должны базироваться на моделях, содержащих параметры, численные значения которых могут переноситься в ряду молекул со сходными структурными группировками.

1. Грибов Л.А., Прокофьева Н.И. Основы физики. Изд. 2, доп. Наука, Главная редакция физ.-мат. литературы, Москва, 1995, 552 с.
2. Грибов Л.А. Дополнительность и доказательность в науке, или о некоторых фундаментальных понятиях и проблемах теории и методов исследования строения и свойств сложных молекул и молекулярных систем. Журнал структурной химии, 1994, т. 35, № 4, с. 123-134.
3. Л.А. Грибов. Философия естественных наук. Учебное пособие для вузов. Ред. С.А. Лебедев. Глава 2. Принципы формирования научного знания на примере физики. С. 35-83.

F2. Теория термических средних колебательных координат [наверх]

Создана теория термических средних колебательных координат молекул по температурному ансамблю в молекулярном идеальном газе. Полученные формулы имеют регулярное поведение при резонансах Ферми для составных частот.

Теория основана на решении интегрального уравнения Блоха для статистической суммы колебательных состояний и позволяет изучать зависимость термических средних от геометрии молекулы и силовых постоянных различного порядка. Её применение важно в рентгенографии, в электронографии и нейтронографии молекулярных систем в газовой и конденсированной фазах вещества.

1. Новосадов Б.К., Кочиков И.В., Тарасов Ю.И. Расчет моментов плотности распределения межъядерных расстояний многоатомных молекул. Журнал физической химии. 2004. Т. 78. №1. С. 44-48.
2. Новосадов Б.К., Кочиков И.В., Тарасов Ю.И. Новый метод расчета моментов термически средней плотности распределения межъядерных расстояний многоатомных молекул с помощью интегрального уравнения Блоха. Журнал структурной химии. 2005. Т. 46. № 5. С. 813-821.
3. Новосадов Б.К., Кочиков И.В., Тарасов Ю.И. Теория и расчет ангармонических поправок второго порядка функции плотности распределения межъядерных расстояний. Журнал физической химии. 2006. Т. 80. № 8. С. 1457-1460.

F3. Уравнение состояния реального газа [наверх]

Предложено новое уравнение состояния реального газа, в котором явно учитываются универсальные взаимодействия между частицами и полученные путём квантовых расчётов усреднённые межмолекулярные потенциалы.

Уравнение не только воспроизводит Ван-дер-Ваальсовы изотермы реального газа, но и раскрывает физическую природу характерных особенностей таких изотерм для области критических состояний.

1. Л.А. Грибов. Простая модель состояния реального газа и жидкости, связывающая микро- и макроописания. Журнал структурной химии, 2006, т. 47, № 2, с. 291-294.

F4. Моделирование процесса эволюции объектов молекулярного мира на ранних стадиях формирования органического вещества [наверх]

Рассмотрен целый ряд проблем, связанных с закономерностями, проявляющимися при анализе процессов, определяющих как явление жизни, так и саму возможность возникновения этого феномена.

F4a. Теория молекулярных процессов и общая картина развития биосферы [наверх]

На базе первых принципов с позиций теории молекулярных превращений проанализирован большой спектр специфических свойств молекулярных объектов и найдены аналогии в поведении молекул и объектов на более высоких стадиях организации материи вплоть до биосферы.

Молекулы (в отличие от, например, кристаллов) обладают способностью воспринимать и единственным образом перерабатывать заданную в нечетком виде входную информацию, а затем направленно передавать ее во внутримолекулярном пространстве на большие расстояния. Показано, как эти действия могут реализовываться в молекулах, и на каких основах могут быть построены молекулярные логические элементы и приемно-преобразующие устройства; рассмотрена проблема комплементарности, обучения и сравнение образов в молекулярном мире.

Исследованы экспериментально наблюдаемые (в спектроскопии и химических превращениях) низкочастотные периодические процессы в молекулах, развита теория таких процессов. На этой основе предложена простая модель эффекта репликации как следствие первых принципов, объяснено появление биологического ритма. Показано, что периодические изменения характеристик внешних воздействий приводят к возникновению общего для всего молекулярного ансамбля ритма (биоритма) и могут выступать как факторы, стимулирующие биохимические процессы и, более того, способные влиять на «направление эволюции» биомолекулярной системы.

Определяющим признаком феномена жизни является связанная с закономерностями эффекта репликации направленная передача информации от прошлого к будущему. Показано, что наличие нескольких путей эволюции при определённых условиях может не только не мешать, но и способствовать выделению преимущественного направления. Эволюционный выбор направления, приводящего к максимальной плотности передачи информации, определяется соотношениями вероятностей рождения и смерти воспроизводимых структур. Необходимое для повышения эффекта самоорганизации уменьшение потока негоэнтропии достигается при увеличении разнообразия воспроизводимых объектов. Задаваемое генетическим кодом выделенное направление эволюции и свойство множественности объектов биосферы находятся во взаимодополняющем соотношении. Сложность мира жизни является необходимым условием развития биосферы в целом.

Таким образом, можно заключить, что современная теория молекулярных процессов позволяет естественным образом объяснить некоторые важнейшие наблюдаемые особенности формирования биосферы на первых этапах появления молекулярного мира.

Принципиально важным общим выводом является то, что возможно построение общей картины развития биосферы на основе первых принципов современной теории строения молекулярных объектов и происходящих в них процессов.

F4b. Эволюция молекулярного мира на ранних стадиях существования Вселенной [наверх]

На основе базового в теории эволюции понятия о причинно-следственных связях сформулированы и физически обоснованы использованные модели эволюционного процесса в форме последовательных цепочек импликаций с обратными связями (кольцевые модели).

Показано, что для существования эволюционных процессов необходимо:

• во-первых, большое разнообразие путей эволюции, а следовательно, нужен рост разнообразия биообъектов
  
  
• во-вторых, существование в системе не только процессов эволюционного усложнения и множественности его этапов, но и разложения сложных структур, т.е. их смерти
  
  
• и в-третьих, существование среды (в частности, в виде электромагнитного поля или излучения), в которой находится и с которой взаимодействует эволюционирующая система. Без среды процессы эволюционных превращений невозможны, причем среда может быть либо в форме поля, либо в форме совокупности материальных объектов (например, водная среда), либо и того, и другого вместе.

Второе начало термодинамики выполняется в процессах эволюционного усложнения систем, а общепринятый вывод о потреблении негэнтропии при таких процессах базируется на использовании результатов для сильно упрощённой модели.

Энтропия внутренних движений элементов системы (энтропия колебаний) определяется, в первую очередь, структурой соединений, а не числом атомов в молекуле и ее атомным составом. Например, для структурных изомеров атомный состав не изменен, а величина энтропии существенно различна. Определяющим для величины энтропии колебательных движений является появление большого числа низкочастотных колебаний (до 500 см^-1), роль высокочастотных колебаний (более 500 см^-1) пренебрежимо мала. Это позволяет ранжировать вероятность появления устойчивых изомерных форм соединений по признаку величины их энтропии.

Показано, что четко проявляется скачок энтропии в ряду трех характерных групп углеводородов: ациклические, циклические с ответвлениями и полициклические соединения. Если считать, что эволюционное развитие совершается в согласии с требованием возрастания энтропии, то естественный вывод заключается в том, что на ранних стадиях наиболее вероятным является появление ациклических структур, а циклические менее вероятны, т.е. присутствуют, но в существенно меньших количествах. Изменение структур молекул идёт в направлении преимущественного образования ациклических структур.

Области (заштрихованы) значений колебательной энтропии для трёх групп углеводородов: ациклические соединения, циклические углеводороды с ответвлениями и (поли)циклические соединения. N_C – число атомов углерода.

Усложнение молекулярного мира с неизбежностью приводит к необходимости возникновения молекул с развитым скелетом, преимущественно формируемым связями примерно той же упругости, что и C–C. Наличие большого числа C=C и C≡C связей невыгодно.

Высокая реакционная избирательность молекул, участвующих в биохимические процессах, невозможна без появления крупных и достаточно "жёстких" структур, что обеспечивает возникновение эффекта "ключ-замок". Показано, что наиболее вероятными и эффективными с этой точки зрения являются спиральные структуры, пространственная упругость которых обеспечивается водородными связями между структурными элементами спирали.

Найденные закономерности согласуются со вторым началом термодинамики. Это означает, что причинно-следственные связи, описывающие общие закономерности эволюции молекулярного мира, являются вполне определёнными и не могут восприниматься как случайные.

1. Грибов Л.А., Баранов В.И. Молекулы и жизнь. В сб. «Проблемы зарождения и эволюции биосферы», под ред. акад. Э.М.Галимова. - М.: Книжный дом «ЛИБРОКОМ», 2008. - с. 33-56.
2. L. Gribov, V. Baranov, Yu. Magarshak. Is "silicate life" possible? Proceeding of ARW NATO Environmental and Biological Risks of Nanobiotechnology, Nanobionics and Hybrid Organic-Silicon Nanodevices (Silicon vs. Carbon). Springer, 2009, p. 1-8.
3. Грибов Л.А., Баранов В.И. Михайлов И.В. Стрела времени на ранних стадиях эволюции биосферы. Детерминизм и множественность. Геохимия. 2012. № 5. С. 435–452.

F5. Лазерная аналитическая спектроскопия [наверх]

В группе лазерной спектроскопии развивались высокочувствительные и селективные методы элементного анализа: «стимулируемая лазером ионизация», «возбуждаемая лазером флуоресценция в графитовых печах» и «лазерная атомно-адсорбционная спектрометрия» с модулируемыми по длине волны диодными лазерами.

Стимулируемая лазером ионизация (СЛИ) использует селективное ступенчатое возбуждение атомов в высоколежащиие электронные состояния с последующей ионизацией и регистрацией электронов или ионов. Техника позволила достичь инструментальных пределов обнаружения 10^-9–10^-14 г/мл, проводить прямой анализ реальных образцов (природные воды, горные породы, высокочистые вещества) в растворах без концентрирования или удаления основы пробы с пределами обнаружения 10^-9–10^-12 г/мл, что на 3-5 порядков ниже, чем в пламенной атомно-адсорбционной спектрометрии. Для щелочных металлов инструментальные пределы обнаружения достигают рекордно-низких значений 10^-13–10^-14 г/мл. Разработаны методики анализа практически важных объектов, в том числе определение:

• In в особо чистом Sn (10^-9%)
• Yb в растворах LuO и TmO (10^-4%)
• Li, Rb, Cs в горных породах (10^-6 - 10^-8%)
• Pb в природных водах (10^-8%)
• Li, Na, K, Cu, Sb в особо чистых ацетоне, изопропаноле, фосфорной кислоте (до 10^-11%)
• Re в технологических растворах (10^-5%)
• In в растворах особо чистого Cd (3•10^-8%)

Системы «стержень-пламя». Разработанные атомизаторы-ионизаторы «стержень-пламя», конструкции которых запатентованы, используют импульсное испарение пробы с графитовой поверхности в пламя, позволяют проводить прямой анализ жидких и твёрдых микропроб без какой-либо пробоподготовки. Возможности этой техники СЛИ продемонстрированы на примерах анализа твердых образцов металла и сплавов: определения Cu в Ge, определения Cs в CdHgTe, определения In в сплаве CdHgTe с пределами обнаружения 10^-8–10^-10%. Созданы опытные образцы СЛИ-спектрометров для анализа жидких и твёрдых проб.

Матрицы. Резонансное многоступенчатое взаимодействие лазерного излучения с атомами обеспечивает высокую селективность, что позволяет существенно уменьшать или совсем исключать влияния основы пробы на аналитический сигнал при анализе реальных объектов. В этих условиях нет необходимости использования стандартных образцов состава и можно использовать калибровку по водным эталонам. Работа в режиме насыщения возбуждаемых переходов позволяет определять коэффициенты атомизации и рассчитать величину аналитического сигнала по параметрам аналитического прибора и определяемого элемента, что является важным шагом к созданию безэталонного анализа.

Возбуждаемая лазером флуоресценция. Создан лазерный флуоресцентный спектрометр с атомизатором переменного давления и интенсифицированной диодной матрицей. Разработаны методики прямого определения Tl в речных водах; Ni и Sb в речных и морских водах, морских осадках; Sb в цельной крови, плазме на уровне ppb-ppt.

Исследование процессов атомизации и возможности создания на основе разработанных техник безэталонного анализа. Разработан новый подход к решению проблемы эффективной атомизации элемента, позволяющий исследовать процессы испарения и атомизации в реальных аналитических условиях в широком диапазоне давлений буферного газа, используя высокочувствительные лазерные методы детектирования атомов и молекул. Изучение процессов атомизации Ag, Ga, In, Cu показало, что разрабатываемый подход позволяет детально исследовать сложные, одновременно протекающие процессы испарения и атомизации и создать методы измерения эффективности атомизации.

Лазерная атомно-абсорбционная спектрометрия с диодными лазерами. Это направление работ связано с техникой лазерной атомно-абсорбционной спектрометрии с использованием модулированных по длине волны диодных лазеров. Она позволяет детектировать аналитические сигналы одновременно из различных областей атомизатора с высокой чувствительностью и получать спектры поглощения исследуемого атома в течение процесса атомизации с временным разрешением порядка 0,1–0,01 сек. На примере атома Rb изучены возможности высокочувствительного определения Rb в графитовой печи на уровне 10 фемтограмм при детектировании 2-ой и 4-ой гармоник абсорбционного сигнала и влияния матриц на аналитический сигнал Rb в различных областях атомизатора.

Молекулярный анализ. Появление новых типов лазеров позволяет развивать принципиально новые подходы к определению молекул. Исследования возможностей лазерного излучения фемтосекундной длительности с помощью техники накачка/зондирование позволило обнаружить процессы возбуждения и релаксации с характерными временами в субпикосекундном и пикосекундном диапазонах. Времена наблюдаемых релаксационных процессов на много порядков меньше времени между столкновениями молекул и могут различаться для разных молекул более чем на порядок. Разница в величине времен релаксации позволяет использовать временную селекцию для детектирования молекул в смесях. Это обеспечивает селективность определения за счёт отстройки от более медленных столкновительных релаксационных процессов и позволяет уменьшить или вовсе исключить влияние основы пробы на аналитическиё сигнал, в перспективе создать безэталонные методы молекулярного анализа, не использующие стандартных образцов состава.

1. Chekalin N.V., Marunkov A.G., Pavlutskaya V.I., Bachin S.V. Determination of traces of Cs, Li and Rb in rocks by LEI without preconcentration. Spectrochim. Acta, 46B, 1991, р. 551-558
2. Chekalin N.V., Pavlutskaya V.I., Vlasov I.I. A Rod-Flame System in Direct LEI Analysis of High-Purity Substances. Spectrochim. Acta 1991, 46B, 1701-1709
3. Chekalin N.V. Vlasov I.I. Direct Analysis of Liquid and Solid Samples Without Sample Preparation Using Laser-Enhanced Ionization. J.Anal.Atom.Spectr. 1992, 7, p 225-228.
4. Chekalin N.V., Axner O., Ljungberg P., Malmsten I. Direct Determination of Thallium in Natural Waters by Laser Induced Fluorescence in Graphite Furnace (LIF GF). Int. J. of Environmental Anal. Chem. 1993, 53, p.185-193
5. Chekalin N., Marunkov A., Axner O. Laser-Induced Fluorescence in Graphite Furnace under Low Pressure Conditions as a Powerful Technique for Studies of Atomization Mechanisms: Investigation of Ag. Spectrochim. Acta, 1994, 49B, p. 1411-1435
6. J. Gustafsson, N. Chekalin, O. Axner. Improved detectability of wavelength modulation diode laser absorption spectrometry applied to window-equipped graphite furnaces by 4th and 6th harmonic detection. Spectrochim. Acta (B), 2003, v. 58, №1, pp. 111-122

F6. Таутомерный состав и таутомерные превращения оснований нуклеиновых кислот [наверх]

Развиты оптические методы определения таутомерного состава молекулярных соединений в разных фазовых состояниях и проведено комплексное исследование прототропной таутомерии ОНК методами теоретической спектроскопии.

Предложена оптимальная и эффективная методика расчета колебательных спектров молекул в конденсированных состояниях, позволяющая определять таутомерный состав вещества и анализировать влияние водородных связей на колебательные и электронные спектры молекулярных соединений.

Предложена новая методика прогнозирования таутомерного состава вещества по спектрам на основе полуэмпирического метода расчета параметра таутомерного равновесия с учетом внутри- и межмолекулярного механизма переноса протона.

Показано, что одной из причин образования комплементарных пар как канонических, так и редких таутомерных форм ОНК является цвиттер-ионный характер механизма переноса протона в димерах 5-замещенных урацила и комплементарных пар в разных фазовых состояниях.

Установлены и обоснованы результатами расчета спектральных свойств веществ структурно-динамические модели таутомеров (более 60) и таутомерный состав ОНК в разных фазовых и электронных состояниях.

1. Тен Г.Н., Бурова Т.Г., Баранов В.И. Спектроскопическое исследование структуры оснований нуклеиновых кислот. Учебное пособие. - Саратов: Изд-во Научная книга, 2004. - 149 с.
2. Тен Г.Н., Бурова Т.Г., Баранов В.И. Квантово-химическое исследование прототропной таутомерии оснований нуклеиновых кислот. Учебное пособие. - Саратов: Изд-во Научная книга, 2008. - 151 с.
3. Тен Г.Н., Баранов В.И. Таутомерия оснований нуклеиновых кислот. Часть I. Колебательные спектры канонических форм оснований нуклеиновых кислот и комплементарных пар в разных фазовых состояниях. – Саратов: Изд-во «Саратовский источник», 2014, 118 с.
4. Тен Г.Н., Баранов В.И. Расчет и анализ времени жизни таутомерных форм тимина и 5-хлорурацила в водных растворах с разными pH. Журн. структ. химии, 2009, т. 50, № 1, с.96-102
5. Тен Г.Н., Баранов В.И. Теоретическое исследование таутомерии аденина, пурина, гуанина и цитозина. Биофизика, 2009, т. 54, № 5, с. 813-819
6. Тен Г.Н., Нечаев В.В., Панкратов А.Н., Баранов В.И. Влияние водородной связи на структуру и колебательные спектры комплементарных пар оснований нуклеиновых кислот. I. Аденин-урацил. Журн. структ. химии, 2010, т. 51, № 3, с. 474-482
7. Тен Г.Н., Нечаев В.В., Панкратов А.Н., Березин В.И., Баранов В.И. Влияние водородной связи на структуру и колебательные спектры комплементарных пар оснований нуклеиновых кислот. II. Аденин-тимин. Журн. структ. химии, 2010, т. 51, № 5, с. 883-889